Esempio

Consideriamo $\mathbf{R}^4$ con il prodotto scalare standard e
$\mathcal{B}=((1,3,0,2),(0,1,0,-1),(1,1,1,3),(0,0,0,1))$ una base. Vogliamo dimostrare che $\mathcal{B}$ non è ortonormale e, a partire da $\mathcal{B}$, vogliamo costruire una base ortonormale attraverso il procedimento di ortogonalizzazione di Gram-Schmidt.
Dimostrare che $\mathcal{B}$ non è una base ortonormale è semplice, infatti gli elementi della base non sono versori:
$\vert\vert(1,3,0,2)\vert\vert=\sqrt{1+9+4}=\sqrt{14}\neq 1$.
Ora ortogonalizziamo la base data:
$\mathbf{w}_{1}:= \frac{\mathbf{v}_{1}}{\vert\vert\mathbf{v}_{1}\vert\vert}=\frac{1}{\sqrt{14}}(1,3,0,2)$;
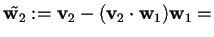
$\tilde{\mathbf{w}_{2}}:=\mathbf{v}_{2}-(\mathbf{v}_{2} \cdot \mathbf{w}_{1})\mathbf{w}_{1}=$
$=(0,1,0,-1)-\frac{1}{\sqrt{14}}(3-2)\frac{1}{\sqrt{14}}(1,3,0,2)=\frac{1}{14}(-1,11,0,-16)$,
da cui
$\mathbf{w}_{2}:= \frac{\tilde{\mathbf{w}_{2}}}{\vert\vert\tilde{\mathbf{w}_{2}}... ...{14}(-1,11,0,-16) \cdot \frac{14}{\sqrt{378}}=\frac{1}{\sqrt{378}}(-1,11,0,-16)$;
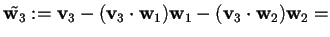
$\tilde{\mathbf{w}_{3}}:=\mathbf{v}_{3}-(\mathbf{v}_{3} \cdot \mathbf{w}_{1}) \mathbf{w}_{1}-(\mathbf{v}_{3} \cdot \mathbf{w}_{2}) \mathbf{w}_{2} =$
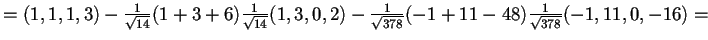
$=(1,1,1,3)-\frac{1}{\sqrt{14}}(1+3+6)\frac{1}{\sqrt{14}}(1,3,0,2)-\frac{1}{\sqrt{378}}(-1+11-48)\frac{1}{\sqrt{378}}(-1,11,0,-16)=$
$=\frac{1}{189}(35,-7,189,-7)$,
da cui
$\mathbf{w}_{3}:= \frac{\tilde{\mathbf{w}_{3}}}{\vert\vert\tilde{\mathbf{w}_{3}}... ...ac{1}{189}(35,-7,189,-7)\frac{\sqrt{189}}{14}=\frac{1}{2\sqrt{189}}(5,-1,27,-1)$;
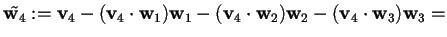
$\tilde{\mathbf{w}_{4}}:=\mathbf{v}_{4}-(\mathbf{v}_{4} \cdot \mathbf{w}_{1}) \m... ...f{w}_{2}) \mathbf{w}_{2}-(\mathbf{v}_{4} \cdot \mathbf{w}_{3}) \mathbf{w}_{3} =$
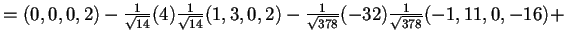
$=(0,0,0,2)-\frac{1}{\sqrt{14}}(4)\frac{1}{\sqrt{14}}(1,3,0,2)-\frac{1}{\sqrt{378}}(-32)\frac{1}{\sqrt{378}}(-1,11,0,-16)+$
$-\frac{1}{2\sqrt{189}}(-2)\frac{1}{2\sqrt{189}}(5,-1,27,-1)=\frac{1}{14}(-5,1,1,1)$,
da cui
$\mathbf{w}_{4}:= \frac{\tilde{\mathbf{w}_{4}}}{\vert\vert\tilde{\mathbf{w}_{4}}\vert\vert}=\frac{1}{14}(-5,1,1,1)\sqrt{7}=\frac{1}{\sqrt{28}}(-5,1,1,1)$.
$\mathcal{C}=(\frac{1}{\sqrt{14}}(1,3,0,2),\frac{1}{\sqrt{378}}(-1,11,0,-16),\frac{1}{2\sqrt{189}}(5,-1,27,-1),\frac{1}{\sqrt{28}}(-5,1,1,1))$ è la base ortonormale cercata.