

- 1.
- Si consideri
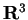 e sia
e sia  la forma bilineare simmetrica definita da:
la forma bilineare simmetrica definita da:
- a)
- Si dica se
 è un prodotto scalare.
è un prodotto scalare.
- b)
- Se la risposta è positiva, si consideri lo spazio vettoriale euclideo con questo prodotto scalare e si dica se la base
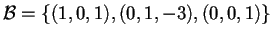 è ortonormale; se non lo è, si determini una base ortonormale.
è ortonormale; se non lo è, si determini una base ortonormale.
Vuoi un aiuto?
Per vedere la soluzione totale, clicca  ,
oppure clicca
,
oppure clicca  per visualizzare ogni singolo passo della soluzione.
per visualizzare ogni singolo passo della soluzione.
Partendo da
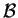 ,
costruiamo una base ortonormale attraverso il procedimento di Gram-Schimdt:
,
costruiamo una base ortonormale attraverso il procedimento di Gram-Schimdt:
prendiamo il primo vettore della base
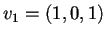 e lo normalizziamo dividendo per la sua norma che abbiamo già trovato sopra:
e lo normalizziamo dividendo per la sua norma che abbiamo già trovato sopra:
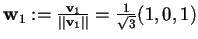 ;
;
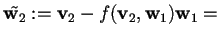
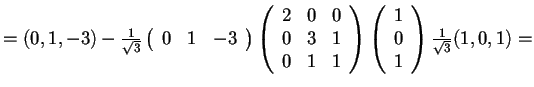
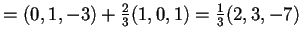 ,
,
da cui, poiché
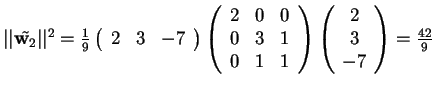 ,
,
si ottiene
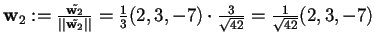 ;
;
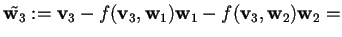
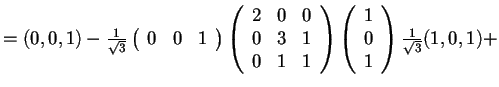
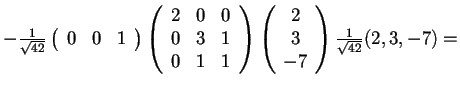
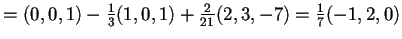 ,
,
da cui, poiché
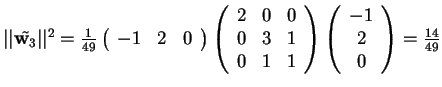 ,
,
si ottiene
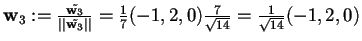 .
.
La base
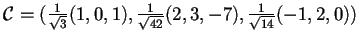 è la base ortonormale cercata.
è la base ortonormale cercata.





e sia
la forma bilineare simmetrica definita da:
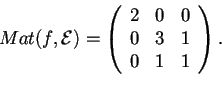
è un prodotto scalare.
è ortonormale; se non lo è, si determini una base ortonormale.
, oppure clicca
per visualizzare ogni singolo passo della soluzione.
Soluzioneè definita positiva, applichiamo il criterio dei minori principali:
;
;
;
è un prodotto scalare.

non è ortonormale, infatti il primo vettore della base non è un versore:
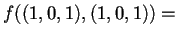
.

, costruiamo una base ortonormale attraverso il procedimento di Gram-Schimdt:
e lo normalizziamo dividendo per la sua norma che abbiamo già trovato sopra:
;
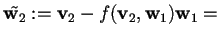
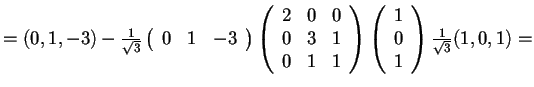
,
,
;
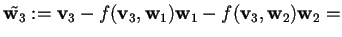
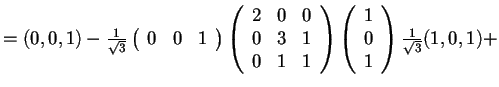
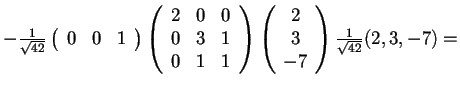
,
,
.
è la base ortonormale cercata.



 Teoria
Teoria