

- 1.
- Dato
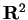 con il prodotto scalare standard, la base
con il prodotto scalare standard, la base
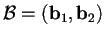 ,
ove
,
ove
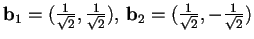 ,
è ortonormale, infatti:
,
è ortonormale, infatti:
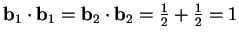 ,
,
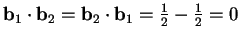 .
.
- 2.
- ATTENZIONE: se una base è ortonormale rispetto ad un prodotto, questo non implica che sia ancora ortonormale rispetto ad un altro prodotto diverso dal precedente!
Ad esempio, la base canonica non è ortonormale per il prodotto scalare su
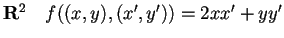 .
.
- 3.
- Consideriamo il prodotto scalare su
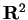 così definito:
così definito:
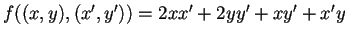 .
.
La base
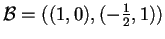 è ortogonale; ne vogliamo cercare una ortonormale.
è ortogonale; ne vogliamo cercare una ortonormale.
Basterà normalizzare i vettori di
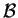 :
allora la nuova base ortonormale sarà:
:
allora la nuova base ortonormale sarà:
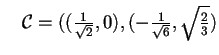 .
.




con il prodotto scalare standard, la base
, ove
, è ortonormale, infatti:
,
.
.
così definito:
.
è ortogonale; ne vogliamo cercare una ortonormale.
:
allora la nuova base ortonormale sarà: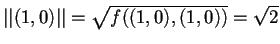
.

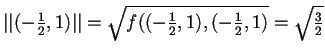

 Teoria
Teoria