Esercizi

1.
Data la forma bilineare simmetrica $g$ su $\mathbf{R}^2\times\mathbf{R}^2$:
a)
$g(\mathbf{x},\mathbf{y})=x_{1}y_{1}+3x_{2}y_{2}-2x_{1}y_{2}-2x_{2}y_{1}$;
b)
$g(\mathbf{x},\mathbf{y})=x_{1}y_{1}+3x_{2}y_{2}$;
si provi che $g$ è un prodotto scalare e si costruisca una base ortonormale rispetto a tale prodotto.

Vuoi un aiuto?
Per vedere la soluzione totale, clicca , oppure clicca per visualizzare ogni singolo passo della soluzione.

Soluzione
Punto a)
I passo:
Prendiamo la matrice associata a $g$ rispetto alla base canonica:

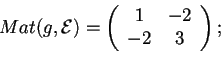
\begin{displaymath}Mat(g,\mathcal{E})= \begin{array}({cc}) 1 & -2\\ -2 & 3 \end{array}; \end{displaymath}

per provare che $g$ è un prodotto scalare dobbiamo dimostrare che è una forma definita positiva, cioè che la sua segnatura è (2,0).
È immediato verificare che il rango è massimo, quindi passiamo a calcolare una base diagonalizzante per $g$. Prendiamo un vettore non isotropo, ad esempio $\mathbf{v}_{1}=(1,0)$, allora sappiamo che
$\mathbf{R}^2=<\mathbf{v}_{1}>\oplus \, \mathbf{v}_{1}^{\perp}$,
ove $\mathbf{v}_{1}^{\perp}=\{ (x,y) \in\mathbf{R}^2 \, \vert \, \begin{array}({cc... ...c}) x\\ y \end{array} =0 \}=\{ (x,y) \in\mathbf{R}^2 \, \vert \, x-2y=0 \}$.
Quindi $\mathbf{v}_{1}^{\perp}=<(2,1)>$; allora la base $\mathcal{C}=((1,0),(2,1))$ è ortogonale per $g$, infatti

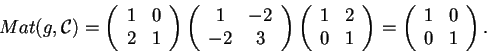
\begin{displaymath}Mat(g,\mathcal{C})= \begin{array}({cc}) 1 & 0\\ 2 & 1 \e... ...d{array}= \begin{array}({cc}) 1 & 0\\ 0 & 1 \end{array}. \end{displaymath}

II passo:  
In particolare, $\mathcal{C}$ oltre ad essere ortogonale è anche ortonormale perché la matrice associata di $g$ rispetto a questa base è la matrice identità, quindi è la base cercata.
Punto b)
I passo:
La matrice associata a $g$ rispetto alla base canonica è:

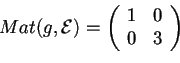
\begin{displaymath}Mat(g,\mathcal{E})= \begin{array}({cc}) 1 & 0\\ 0 & 3 \end{array} \end{displaymath}

che è diagonale di segnatura (2,0); quindi $g$ è un prodotto scalare.
II passo:  

La base $\mathcal{E}$ è già ortognale per $g$, quindi basterà normalizzarla;
allora svolgendo i calcoli si ottiene:
$\vert\vert\mathbf{v}_{1}\vert\vert^2= \begin{array}({cc}) 1 & 0 \end{array} ... ...c}) 1 & 0\\ 0 & 3 \end{array} \begin{array}({c}) 1\\ 0 \end{array} =1$;
$\vert\vert\mathbf{v}_{2}\vert\vert^2= \begin{array}({cc}) 0 & 1 \end{array} ... ...c}) 1 & 0\\ 0 & 3 \end{array} \begin{array}({c}) 0\\ 1 \end{array} =3$;
da cui
$\mathcal{B}=((1,0),\frac{1}{\sqrt{3}}(0,1))$
è la base ortonormale cercata.