Matrici delle forme bilineari

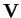
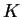
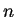
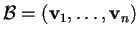
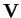
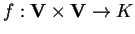
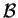
Definizione 2.1   Sia $\mathbf{V}$ un $K$-spazio vettoriale di dimensione $n$ finita, sia $\mathcal{B}=(\mathbf{v}_1,\ldots,\mathbf{v}_n)$ una base per $\mathbf{V}$ e $f: \mathbf{V} \times \mathbf{V} \rightarrow K $ una forma bilineare, allora la matrice di f rispetto a $\mathcal{B}$ è la matrice

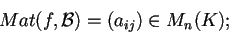 \begin{displaymath} Mat(f,\mathcal{B})= (a_{ij})\in M_n(K); \end{displaymath} (1)

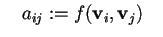
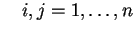
dove $\quad a_{ij}:= f(\mathbf{v}_i,\mathbf{v}_j) \quad$per $ \quad i,j= 1,\ldots,n$.

E' interessante vedere come nel caso della forma simmetrica standard possiamo scrivere la relazione
$f(\mathbf{x},\mathbf{y})= X^{t}Y = x_{1}y_{1}+\cdots+x_{n}y_{n}$
che segue direttamente dalla seguente proposizione:

Proposizione 2.2   Sia $\mathbf{V}$ un $K$-spazio vettoriale di dimensione finita $n$, sia $\mathcal{B}=(\mathbf{v}_1,\ldots,\mathbf{v}_n)$ una base per $\mathbf{V}$, sia $f$ una forma bilineare su $\mathbf{V}$ e siano $\mathbf{v}=(x_{1},\ldots,x_{n})_{\mathcal{B}}$ e $\mathbf{w}=(y_{1},\ldots,y_{n})_{\mathcal{B}}$, allora
$f(\mathbf{v},\mathbf{w})= X^{t} Mat(f,\mathcal{B}) Y$

\begin{displaymath}\textrm{dove} \quad Y= \begin{array}({c}) y_{1}\\ \vdots\... ...}= \begin{array}({ccc}) x_{1} & \ldots &x_{n} \end{array}. \end{displaymath}

Dimostrazione

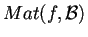
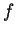
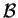
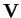
Proposizione 2.3   La matrice $Mat(f,\mathcal{B})$ individua univocamente la forma bilineare $f$, infatti presa una base $\mathcal{B}$ di $\mathbf{V}$, l'applicazione
$Mat(*,\mathcal{B}): Bil(\mathbf{V}) \rightarrow M_{n}(K)$
$\qquad \qquad \qquad f \rightarrow Mat(f,\mathcal{B})$
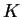
è un isomorfismo di $K$-spazi vettoriali.
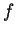
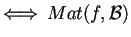
In particolare avremo che la forma $f$ è simmetrica (rispettivamente, antisimmetrica) $\Longleftrightarrow \, Mat(f,\mathcal{B})$ è simmetrica (rispettivamente, antisimmetrica).

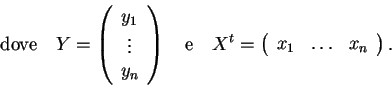
Dimostrazione

Osservazione 2.4   Dalla proposizione (2.3) si deduce anche che
$\dim \, Bil(\mathbf{V})= \dim \, M_{n}(K)= n^2$.