Introduzione alle forme bilineari

$\qquad$ Vogliamo studiare dal punto di vista dell'algebra lineare, come si passa dalla geometria affine ad una struttura più rigida e cioè quella euclidea; esaminando perciò tutte quelle proprietà geometriche che discendono direttamente dalle nozioni di natura metrica, quali angoli, perpendicolarità, distanza.
Per fare ciò dobbiamo studiare quella parte dell'algebra lineare, la teoria delle forme bilineari e quadratiche, tramite la quale si definiscono i suddetti concetti metrici.

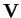
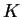
Definizione 1.1   Sia $\mathbf{V}$ un $K$-spazio vettoriale. Un'applicazione di insiemi
$f: \mathbf{V} \times \mathbf{V} \rightarrow K $
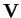
è detta forma bilineare su $\mathbf{V}$ se è lineare in entrambi gli argomenti, cioè se data
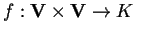
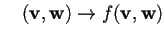
$f:\mathbf{V} \times \mathbf{V} \rightarrow K \quad$ ove $\quad(\mathbf{v},\mathbf{w}) \rightarrow f(\mathbf{v},\mathbf{w})$,
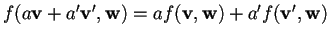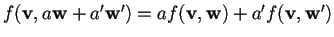
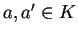
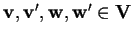
valgono: per ogni $a,a'\in K$ e per ogni $\mathbf{v},\mathbf{v}',\mathbf{w},\mathbf{w}'\in \mathbf{V}$.
Inoltre possiamo distinguere due particolari tipi di forme bilineari:
-
Una forma bilineare si dice simmetrica se
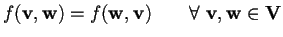
$f(\mathbf{v},\mathbf{w})= f(\mathbf{w},\mathbf{v})\qquad \forall~ \mathbf{v},\mathbf{w}\in \mathbf{V}$.
-
Una forma bilineare si dice antisimmetrica se
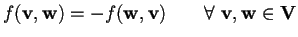
$f(\mathbf{v},\mathbf{w})=-f(\mathbf{w},\mathbf{v})\qquad \forall~ \mathbf{v},\mathbf{w}\in \mathbf{V}$.
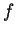
In particolare, se $f$ è antisimmetrica, allora
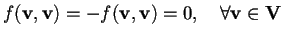
$f(\mathbf{v},\mathbf{v})= -f(\mathbf{v},\mathbf{v})=0, \quad \forall \mathbf{v} \in \mathbf{V}$.

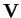
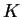
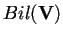
Proposizione 1.2   Le seguenti operazioni danno all'insieme delle forme bilineari su $\mathbf{V}$ una struttura di $K$-spazio vettoriale, denotato con $Bil(\mathbf{V})$:
1.
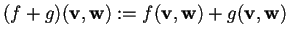$(f+g)(\mathbf{v},\mathbf{w}):= f(\mathbf{v},\mathbf{w})+g(\mathbf{v},\mathbf{w})$;
2.
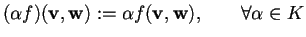$(\alpha f)(\mathbf{v},\mathbf{w}):= \alpha f(\mathbf{v},\mathbf{w}), \qquad \forall \alpha \in K$.

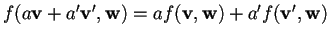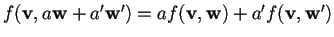
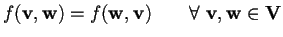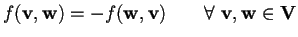Dimostrazione