

- 1.
- Un esempio banale è la forma bilineare
nulla:
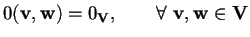
.
In particolare si noti che è sia simmetrica che antisimmetrica.
- 2.
- Se
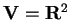 ,
allora la funzione
,
allora la funzione
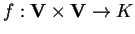 ,
con
è bilineare.
,
con
è bilineare.
- 3.
- Se
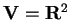 ,
allora la funzione
,
allora la funzione
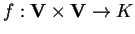 ,
con
non è bilineare, infatti
,
con
non è bilineare, infatti
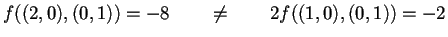
- 4.
- Consideriamo una matrice
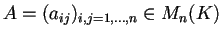 e
e 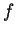 definita da:
definita da:
ove
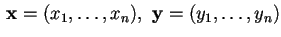
.
Osserviamo che quindi un polinomio biomogeneo di grado 1 nelle
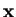 e nelle
e nelle
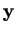 definisce una forma bilineare.
definisce una forma bilineare.
Se in particolare abbiamo che 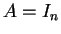 ,
allora
,
allora
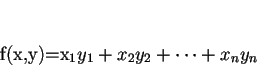 |
(1) |
La 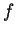 è una forma bilineare simmetrica detta forma simmetrica standard su
è una forma bilineare simmetrica detta forma simmetrica standard su 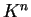 .
.
- 5.
- Se
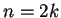 e considero
e considero
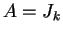 dove
dove
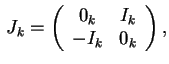 allora avremo
allora avremo
che è una forma bilineare alterna detta forma alterna standard su K.




.
, allora la funzione
, con
è bilineare., allora la funzione
, con
non è bilineare, infatti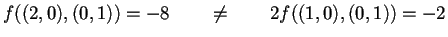
e
definita da:
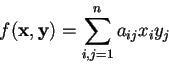
.
e nelle
definisce una forma bilineare.
, allora
è una forma bilineare simmetrica detta forma simmetrica standard su
.
e considero
dove
allora avremo
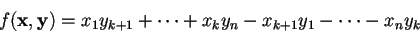

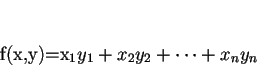

 Teoria
Teoria