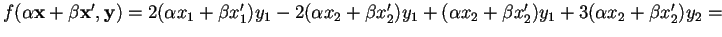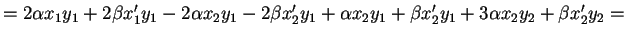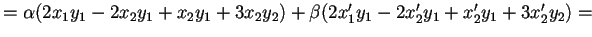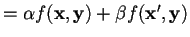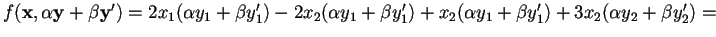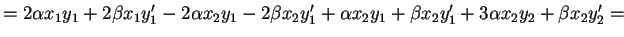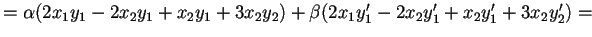Esercizi
Dimostrare che le seguenti forme sono bilineari:
Vuoi un aiuto?
- 1.
;
- 2.
;
- 3.
.
Per vedere la soluzione totale, clicca, oppure clicca
per visualizzare ogni singolo passo della soluzione.
- 3.
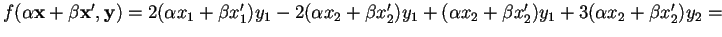
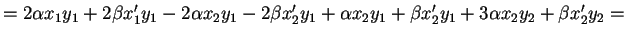
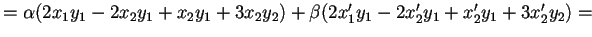
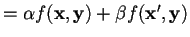
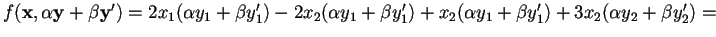
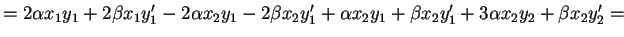
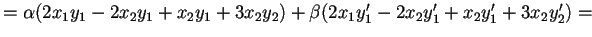


Esercizi
Dimostrare che le seguenti forme sono bilineari:
Vuoi un aiuto?
- 1.
;
- 2.
;
- 3.
.
Per vedere la soluzione totale, clicca, oppure clicca
per visualizzare ogni singolo passo della soluzione.
- 3.