
Esercizi

Vuoi un aiuto?
- 1.
- Si consideri la seguente forma bilineare:
e si determini la matrice associata dirispetto alla base canonica
, a
e a
.
Per vedere la soluzione totale, clicca, oppure clicca
per visualizzare ogni singolo passo della soluzione.
Soluzione
- I passo:
- Determinare la matrice rispetto alla base canonica è immediato, infatti basta inserire nella matrice
il coefficiente di
nella posizione
, cioè:
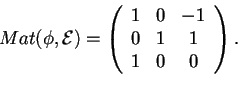
II passo: Il terzo caso con
Il terzo caso conè analogo al precedente, infatti dobbiamo calcolare:
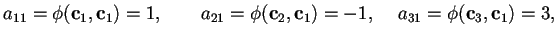
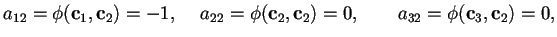
Da ciò segue che
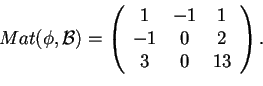

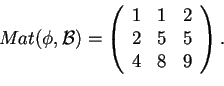


 Teoria
Teoria