A questo punto, dopo aver presentato le alternative non-gaussiane alla finanza moderna, passiamo ad una parte di verifica nella quale, utilizzando le diverse tecniche per la stima del rischio, cercheremo di verificare l'accuratezza dei modelli proposti.

 

 

VaR: l'Unita' di Stima del Rischio

Nell'industria finanziaria di oggi l'unità di misura più utilizzata per quantificare il suddetto tipo di rischio è il Value-at-Risk (VaR) che, grazie al fatto di poter riassumere il valore del rischio in un solo numero, si e' imposto come il più diffuso.

 

 

 

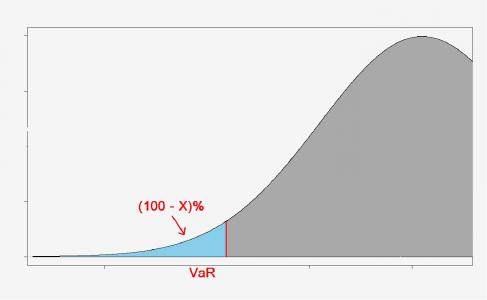
Il concetto di VaR risponde alla domanda di quale sia la perdita massima possibile per un titolo in un periodo t, espressa con un dato livello di probabilità' X%; il parametro temporale t può assumere valori arbitrari ma nella maggior parte dei casi si utilizza un valore pari a 1 giorno. Per calcolare il coefficiente di rischio in VaR si possono utilizzare svariati metodi ma i tre più comuni sono:

 

• Parametrico: poggia sull'assunto di una distribuzione gaussiana dei rendimenti e sulla linearità delle combinazioni dei titoli in un portfolio;

• Simulazione storica: assume che il rendimento futuro sarà uguale a quello di uno dei giorni del database delle serie storiche;

• Simulazioni di Monte Carlo: funziona come il metodo della simulazione storica, ma la previsione sui rendimenti futuri viene fatta attraverso un generatore di numeri pseudocasuali, invece che utilizzando le serie storiche.

Non si deve pensare ai 3 metodi come equivalenti o cercare di determinare quale sia il migliore; è interessante, invece, notare come tutti e 3 risolvano il problema della stima del rischio ma in modi diversi e sono da utilizzare in situazioni diverse. Per completezza e' comunque necessario aggiungere che il metodo di stima del rischio in VaR non è né l'unico né il più accurato e presenta alcuni punti deboli.