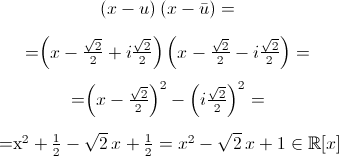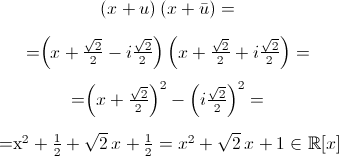Soluzione
24.
- In
forma trigonometrica -i=cos(3π/2)+sen(3π/2).
Quindi le radici quadrate complesse di -i sono
due, una con argomento (1/2)(3π/2)=3π/4
e l'altra con argomento (1/2)(3π/2 +
2π)=7π/4, entrambe con modulo unitario.
Quella
con parte reale maggiore di 0 (in rosso in figura) è u=cos(7π/4)+i·sen(7π/4)=√2/2-i√2/2.
- e (c).
Poichè u2=-i,
si ha: u4=-1 ⇒ u4+1=0
x4+1
è un polinomio a coefficienti interi e dunque razionali, monico ed irriducibile (vedi sotto) e che
si annulla in u, dunque polinomio minimo
di u su Q:
pu(x)=x4+1
Irriducibilità di pu. Quindi si ha: pu(u)=pu(-u)=pu(ū)=pu(-ū)=0.
Poichè in pu
compaiono solo potenze pari di x, se a
è una radice lo è anche -a.
Poichè pu
è un polinomio a coefficienti reali, se a
è una radice lo è anche 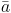 , dove
, dove 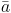 è il complesso coniugato di a.
O, se preferite, le quattro radici quarte di -1 sono le radici di pu.
Si ha:
è il complesso coniugato di a.
O, se preferite, le quattro radici quarte di -1 sono le radici di pu.
Si ha:
u=√2/2-i√2/2 -u=-√2/2+i√2/2 ū=√2/2+i√2/2 -ū=-√2/2-i√2/2
e su C x4+1=(x-(√2/2-i√2/2))(x-(-√2/2+i√2/2))(x-(√2/2+i√2/2))(x-(-√2/2-i√2/2)).
Poichè
nessuna delle quattro radici è reale, non si
ha un fattore lineare in R[x]
e quindi neanche in Q[x].
Su R si
hanno due
fattori quadratici con delta negativo:
e:
Ricordiamo
infatti che per ogni α complesso: (x-α)(x-ᾱ)=x²-2Re(αx)+∣α∣²∈R[x].
Quindi su R
x4+1=(x2-√2x+1)(x2+√2x+1).
Su Q
abbiamo già visto che x4+1
non ha fattori lineari, quindi se non è irriducibile si deve
scomporre come prodotto di due polinomi irriducibili di secondo grado.
Ma questi comparirebbero allora anche nella fattorizzazione su R.
Quindi x4+1 è
irriducibile su Q.
- L'estensione
di campi Q(u)/Q ha grado 4 come il grado di x4+1
ed una base di Q(u)
su Q
è: {1, u, u2, u3}={1,
√2/2-i√2/2, -i, √2/2+i√2/2}={1,
u, -i, ū}. Tutte e quattro le radici del polinomio
appartengono all'estensione (cioè: Q(u)=Q(u,-u,ū,-ū))
ed x4+1 spezza su Q(u)
in fattori lineari, quindi Q(u)
è campo di
spezzamento di pu
su Q.
Torna
agli esercizi.
Torna
alla teoria.
Vai
all'esercizio 25.

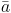 , dove
, dove 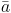 è il complesso coniugato di a.
O, se preferite, le quattro radici quarte di -1 sono le radici di pu.
Si ha:
è il complesso coniugato di a.
O, se preferite, le quattro radici quarte di -1 sono le radici di pu.
Si ha: