Soluzione 21.


  1.  

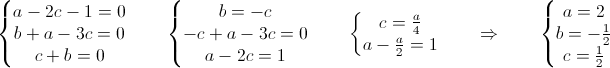
f∈Z[x] ed è monico, quindi le sue radici in Q possono solo essere numeri interi che dividono il termine noto

cioè ±1, ±2, ma nessuno di questi è radice di f. Quindi f è irriducibile su Q, per cui è il polinomio minimo di u, e [Q(u):Q]=3. Si ha: u2∈Q(u) implica Q(u2)⊆Q(u) e u2 ha grado 1 o 3 su Q. Se [Q(u2):Q]=1, allora: u2∈Q e quindi u è radice di x2-u2 cioè ha grado 2 su Q (contraddizione).

Se [Q(u2):Q]=3, Q(u2) è un sottospazio di Q(u) di dimensione 3 da cui: Q(u2)=Q(u).




  1. Si ha:



a+bu+cu2+au+bu2+cu3-1=0

a+bu+cu2+au+bu2+c(-3u-2)-1=0






  1. Sia g di grado 4 irriducibile su Q. Se g non è irriducibile su Q(u), g ha un fattore lineare oppure g=hq con h e q di grado 2 irriducibili su Q(u). Ma se ha un fattore lineare allora ha una radice ω in Q(u), e per quanto detto in (a) ω∈Q (che non è possibile altrimenti g è riducibile su Q) oppure ω ha grado 3 su Q e se ω∈C è radice di un polinomio irriducibile di grado 4 su Q deve avere grado 4 su Q. Quindi f=hq con h e q di grado 2 irriducibili su Q(u).

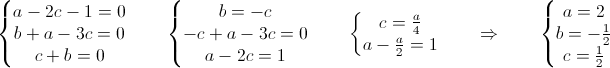
Sia v∈C radice di h; allora Q(u)(v) è una estensione di grado 6 di Q. Ma v è radice anche di f, quindi Q(v) ha grado 4 su Q. Quindi Q(u)(v)=Q(u,v) è tale che:


6=[Q(u,v):Q]=[Q(u,v):Q(v)][Q(v):Q]

[Q(v):Q]=4 e 4 non divide 6.



Torna agli esercizi.

Torna alla teoria.

Vai all'esercizio 22.