Calcolare la somma della serie
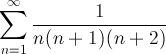
Procediamo con la decomposizione dei termini della serie:
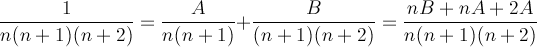
Da tale identità estrapoliamo le relazioni 2A = 1 e nA = -nB che ci permettono di riscrivere la serie data come:
![sum [1/(n(n+1)(n+2))]= sum [1/(2n(n+1))-1/(2(n+1)(n+2))]](../img/es2c2.gif)
che è ancora una volta una serie telescopica.
Infatti, valutiamo più nel dettaglio Sn:
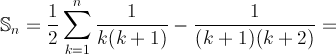
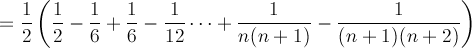
ovvero
![S_n = 1/2[1/2 - 1/((n+1)(n+2))]](../img/es2c5.gif)
e passando al limite per n che tende ad infinito otteniamo:
![lim S_n = 1/4 - lim [1/((n+1)(n+2))]](../img/es2c6.gif)
che è proprio la somma cercata.
