Determinare per quali valori del parametro reale
le seguenti serie sono convergenti
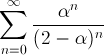
Osserviamo preliminarmente che se alfa è nullo allora
abbiamo a che fare con la serie nulla che è convergente con somma zero, se invece
= 2 non risulta
definito tale rapporto poichè ovviamente si annulla il denominatore.
Sia dunque diverso da zero e da due, si ha:
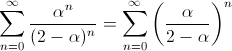
che riconosciamo immediatamente essere la serie geometrica di ragione:
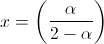
che sappiamo essere convergente se |x| < 1 ovvero se:
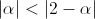
Per tanto, risolvendo la disequazione,
otteniamo che la serie data risulta convergente se < 1.