Serie Numeriche

Determinare per quali valori del parametro reale le seguenti serie sono convergenti

Studiamo preliminarmente la convergenza assoluta che equivale a studiare la convergenza della serie:

Il cui termine n-esimo possiamo riscriverlo come:

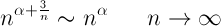
Poiché sappiamo che la serie

per il criterio del confronto, anche la serie data converge assolutamente se < -1.

Il caso della convergenza semplice è decisamente più complicato e richiede gli strumenti del calcolo differenziale.
Consideriamo quindi > -1 e valutiamo innanzi tutto per quali valori di risulti verificata la condizione necessaria per la convergenza.

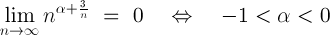
Quindi se riusciamo a mostrare che per appartenente all'intervallo ]-1,0[ è applicabile il criterio di Leibnitz, ciò proverebbe che la serie data è semplicemente convergente.

Si tratta quindi di mostrare che:

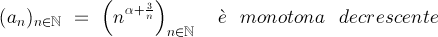
Per fare questo studiamo la funzione:

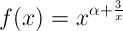
la cui derivata è

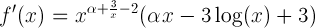
e per chi avesse bisogno di delucidazioni può trovare tutti i passaggi qui.

Tale derivata è negativa per tutti gli nell'intervallo considerato, come mostra anche il grafico che trovate qui

Ne consegue che la funzione è decrescente, così come la successione da cui eravamo partiti. Per tanto, in virtù del criterio di Leibnitz, la serie data converge semplicemente per < 0.