Determinare per quali valori del parametro reale
le seguenti serie sono convergenti
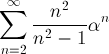
Osserviamo preliminarmente che per = 0,
si ha la serie nulla che ovviamente è convergente con somma zero.
Osserviamo inoltre che il rapporto che compare a sinistra delle potenze di
è sempre diverso da zero,
ergo possiamo applicare il criterio del rapporto. Si ha:
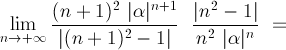
Semplificando le potenze di
ed eliminando i valori assoluti dei termini di cui conosciamo il segno otteniamo:
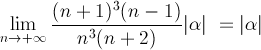
Quindi tale limite esiste sempre finito per ogni alfa reale e per il criterio del rapporto sappiamo che la serie data è assolutamente convergente se
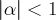
Per = 1
il criterio è inefficace
ma il calcolo del limite porge
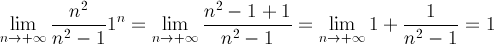
e quindi non essendo infinitesimo, non risulta soddisfatta la condizione necessaria alla convergenza e per tanto la serie diverge.
Per = -1
invece la serie data è a termini alterni e poiché non esiste
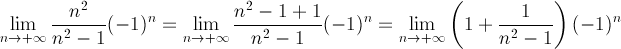
ancora una volta, non essendo soddisfatta la condizione necessaria per la convergenza, la serie non converge.