Dimostrazione:
Sappiamo dal teorema spettrale che esiste una matrice
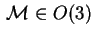 tale che tale che
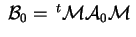 è una matrice
diagonale; gli elementi diagonali di è una matrice
diagonale; gli elementi diagonali di
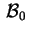 sono
gli autovalori di sono
gli autovalori di
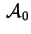 . Supponiamo che la quadrica
abbia un centro . Supponiamo che la quadrica
abbia un centro 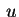 , cosicchè se , cosicchè se
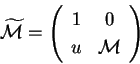 allora
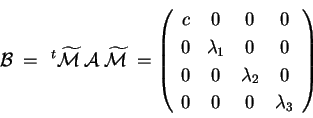
per un certo
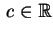 . Ora . Ora
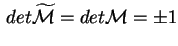 , e quindi
Se la quadrica è non degenere, e quindi , e quindi
Se la quadrica è non degenere, e quindi
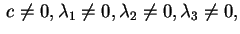 questo dà una
comoda formula per questo dà una
comoda formula per 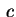 , ossia , ossia
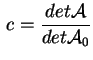 . .
L'equazione diventa
e quindi, moltiplicando per
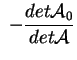 , otteniamo l'asserto. , otteniamo l'asserto.
Se invece
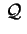 non ha centro allora il rango di non ha centro allora il rango di
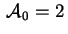 quindi un autovalore è nullo. Supponiamo
sia quindi un autovalore è nullo. Supponiamo
sia
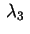 . Esiste un riferimento ortonormale rispetto
al quale la quadrica ha matrice
con . Esiste un riferimento ortonormale rispetto
al quale la quadrica ha matrice
con 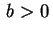 . Scambiando la prima e l'ultima colonna possiamo
calcolare che
da cui . Scambiando la prima e l'ultima colonna possiamo
calcolare che
da cui
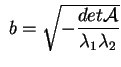 . .
Dal calcolo del polinomio caratteristico di
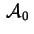 si vede che il prodotto
si vede che il prodotto
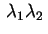 è uguale
all'opposto del coefficiente di grado 1. Se chiamo è uguale
all'opposto del coefficiente di grado 1. Se chiamo
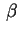 questo coefficiente abbiamo che
questo coefficiente abbiamo che
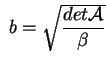 . .
|
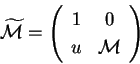 allora
allora
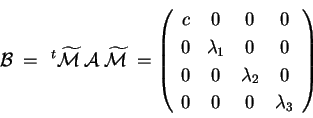
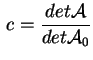 .
.
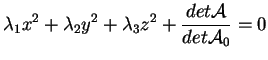
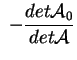 , otteniamo l'asserto.
, otteniamo l'asserto.
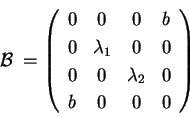
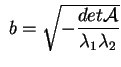 .
. 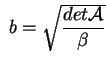 .
.
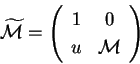 allora
allora
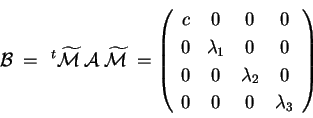
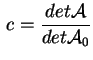 .
.
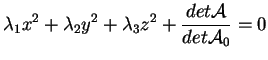
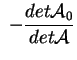 , otteniamo l'asserto.
, otteniamo l'asserto.
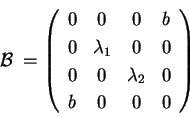
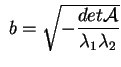 .
. 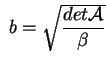 .
.