Le geometrie non euclidee > Due giuristi alle prese con la geometria: Fernand Karl Schweikart e Franz Adolph Taurinus

Due giuristi alle prese con la geometria: Fernand Karl Schweikart e Franz Adolph Taurinus

E' significativo notare che tentativi di stabilire un sistema geometrico non euclideo venivano allora da ambienti estranei al mondo matematico.

Il giurista Fernand Karl Schweikart (1780-1859), dopo aver pubblicato un libro di geometria euclidea nel 1807, si dedicò a ricerche sulla teoria delle parallele e raggiunse notevoli risultati. Nel 1818 egli mostrava a Gauss alcuni suoi appunti in cui sosteneva l'esistenza di "due tipi di geometria - una geometria in senso ristretto, la euclidea; ed una seconda geometria astrale (astralische Grossenlehre)" in cui i triangoli "hanno la particolarità che la somma dei loro tre angoli non è uguale a due angoli retti" ed "è tanto più piccola quanto più è grande l'area del triangolo".
Schweikart affermava inoltre che "l'altezza di un triangolo rettangolo isoscele, pur crescendo al crescere dei lati, tuttavia non può superare un certo segmento che io chiamo costante", e concludeva che la "geometria euclidea vale nell'ipotesi che la costante sia infinitamente grande".
La geometria euclidea risultava dunque essere un caso limite della più generale geometria astrale.

Gauss era completamente d'accordo con queste idee e faceva sapere a Schweikart che la comunicazione avuta gli aveva procurato "un piacere straordinario" e affermava di "poter risolvere completamente tutti i problemi della geometria astrale così come è stata finora sviluppata, non appena fosse data la costante C "
A quell'epoca infatti Gauss aveva già maturato le sue idee su quella che, discutendo con l'allievo Friedrich Wachter (1792-1817), aveva chiamato geometria anti-euclidea.

In una lettera del 28 aprile 1817 Gauss scriveva all'amico Heinrich Olbers:
 
Mi sto convincendo sempre di più che la necessità della nostra geometria non può essere dimostrata, almeno non dalla mente umana né per la ragione umana. Forse in una altra vita perverremo ad altre concezioni sulla natura dello spazio, che ora ci sono irraggiungibili. Fino ad allora si deve annoverare la geometria non con l'aritmetica, che è puramente a priori, ma piuttosto con la meccanica.

 
Il giudizio favorevole di Gauss aveva convinto Schweikart a proseguire le ricerche sulla geometria astrale, alle quali esortò il nipote Franz Adolph Taurinus (1794-1874), anch'egli giurista.
Taurinus era fortemente convinto della necessità del postulato euclideo e della possibilità di dimostrarlo. Nella Theorie der Parallellinien (Teoria delle parallele), pubblicata nel 1825, presentava sviluppi analoghi a quelli di Saccheri e di Lambert e determinava la costante di Schweikart, ma ribadiva il suo rifiuto per l'ipotesi dell'angolo acuto -pur riconoscendo che non ne derivavano contraddizioni- poiché "ripugna ogni intuizione" dello spazio.
L'anno successivo Taurinus ripubblicava le sue ricerche, perfezionandole, nei Geometriae prima elementa cui allegava un'appendice sugli sviluppi deducibili dall'ipotesi dell'angolo acuto; risultati che egli congetturava essere forse possibili in qualche sorta di geometria.
Il giovane giurista otteneva tra l'altro la formula fondamentale di una nuova geometria che egli chiamava "logaritmico-sferica", per cui la somma degli angoli di un triangolo era minore di p e al tendere dei lati del triangolo a zero la somma tendeva a p e i triangoli differivano sempre meno da quelli euclidei. 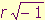Le formule della nuova trigonometria si potevano ottenere da quelle dell'usuale trigonometria sferica considerando immaginario il lato della sfera (cioè ponendo al posto di r).
 
Quando Taurinus pubblicava i frutti delle sue ricerche, Gauss era impegnato sullo studio delle proprietà infinitesimali delle superfici. Nel 1827 pubblicò le Disquisitiones generales circa superficies curvas, un articolo che rappresenta una pietra miliare nella storia delle geometria differenziale, in cui introduceva l'idea decisiva di studiare la geometria di una superficie da un punto di vista intrinseco.
Ovvero di considerare una superficie non come immersa in uno spazio tridimensionale e rappresentata da un'equazione del tipo z = f(x,y), ma piuttosto di "considerare le superfici non come contorni di corpi, ma come corpi di cui una dimensione è infinitamente piccola", una sorta di velo "flessibile ma inestensibile" e deformabile senza pieghe o stiramenti.
Gauss dedicava poi l'ultima parte del suo lavoro ad un dettagliato confronto tra gli angoli di un triangolo geodetico su una superficie e gli angoli di un triangolo piano avente i lati della stessa lunghezza.
In questa occasione egli riportava le misurazioni da lui eseguite per un triangolo avente come vertici le cime dei monti Brocken, Hohehagen e Inselberg, dove la differenza della somma degli angoli da p poteva considerarsi trascurabile. [approfondisci]