Le geometrie non euclidee > Due giuristi alle prese
con la geometria: Schweikart e Taurinus >
Le misurazioni di Gauss
|
Le
misurazioni di Gauss
Nel 1820 Gauss fu incaricato di un progetto di rilevamento
cartografico dello stato tedesco dell'Hannover.
Doveva rilevare enormi triangoli i cui vertici erano costituiti
da campanili o cime di montagne, che erano visibili nonostante
la curvatura terrestre. (E' interessante notare che lo studio
della geometria di Gauss cominciò proprio dall'origine
storica alla quale si fa risalire il termine stesso di geometria,
cioè la misura della Terra).
Gauss costruì uno speciale strumento che gli permetteva
di riflettere la luce del sole in una direzione controllabile
con molta precisione dall'operatore che poteva finemente regolare
lo specchio di cui lo strumento era dotato.
Venne misurato ogni triangolo più volte e dei risultati
ottenuti -leggermente diversi- si fece la media. |
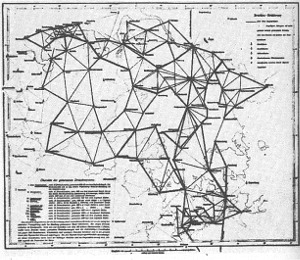 |
Il
procedimento classico usato nell'esecuzione di un rilievo
geodetico si chiama "triangolazione". Si scelgono
un certo numero di punti di riferimento nel paesaggio e si
misurano con cura le distanze fra coppie diverse di punti
di riferimento. La regione di cui si esegue il rilievo viene
ricoperta da una rete di triangoli i cui lati e i cui angoli
vengono determinati attraverso strumenti di misurazione nel
modo più preciso possibile. E' un'operazione relativamente
semplice e noiosa che porta via molto tempo ed è soggetta
a errori. Da questa enorme mole di dati bisogna dedurre le
distanze, in linea d'aria, di punti inaccessibili uno dall'altro.
|
Gauss riferì i risultati relativi
al più grande di quei triangoli (quello che aveva come
vertici le cime dei monti Hohenhagen, Brocken, Inselberg)
a conclusione di uno scritto del 1827: Disquisitiones
generales circa superficies curvas. La sua conclusione
era che, nei limiti di precisione degli strumenti, la somma
degli angoli era 180°. Ovvero che il triangolo terrestre
che ha per vertici le colline di Brocken, Hohehagen e Inselberg
si comporta agli effetti pratici come un triangolo su un foglio
piano, poiché l'errore che si commette è impercettibile.
Il fine dichiarato da Gauss era di confrontare il triangolo
rettilineo giacente nel piano che passa per le tre cime delle
montagne (i tre vertici) con il corrispondente triangolo curvilineo
tracciato al di sotto del primo sulla superficie terrestre.
Le misurazioni di Gauss sono una conferma sperimentale del
V postulato, ma non certo una dimostrazione. La matematica
ha, infatti, criteri ben diversi da quelli delle scienze sperimentali:
in matematica le lunghezze sono definite ed esatte, ma nessuno
strumento può misurare la lunghezza di un oggetto fisico
con precisione superiore a poche cifre decimali.
Il risultato di una misurazione non è mai un numero
esatto, ma piuttosto un intervallo numerico; così una
lunghezza misurata non è una lunghezza nel senso matematico
del termine.
Le misurazioni del triangolo gigante dunque non dimostrano
il V postulato e in generale nessuna misurazione di un triangolo
potrà mai dimostrarlo perché, per quanto si
possano ridurre, gli errori sperimentali non si potranno mai
eliminare completamente.
|
|
|