Le geometrie non euclidee > Due giuristi alle prese
con la geometria: Schweikart e Taurinus >
Disquisitiones generales circa superficies curvas
|
Disquisitiones
generales circa superficies curvas.
Per capire il pensiero di Gauss esaminiamo,
sia pure in modo molto superficiale, i risultati teorici sullo
studio delle superfici curve pubblicati in un saggio del 1827
intitolato Disquisitiones generales circa superficies
curvas.
Vediamo i principali paletti teorici dei
suoi studi.
Una superficie, come per esempio quella della
Terra, può essere pensata immersa in uno spazio tridimensionale
e studiata con i classici metodi della geometria analitica
cartesiana, utilizzando tre coordinate x, y, z; oppure
può essere descritta utilizzando due coordinate curvilinee
u, v. Nel caso della superficie terrestre queste
sono la longitudine e la latitudine.
|
| La latitudine è
la distanza angolare di un punto dall'Equatore, misurata
in gradi e frazioni di grado, sull'arco di meridiano
passante per quel punto. Alla misura in gradi bisogna
aggiungere N o S a seconda che il punto si trovi nell'emisfero
boreale o in quello australe.
La longitudine è la distanza angolare di un punto
dal meridiano di riferimento, o meridiano zero, che
è quello passante per Greenwich, misurata in
gradi e frazioni di grado, sull'arco di parallelo passante
per quel punto. Alla misura in gradi bisogna aggiungere
E o W a seconda che il punto si trovi a Est o a Ovest
del meridiano fondamentale.
|
|
|
| Gauss non utilizza l'equazione
cartesiana del tipo f(x,y,z)=0, ma le equazioni
parametriche
|
x=x(u,v);
y=y(u,v); z=z(u,v) |
dove u e v sono le coordinate curvilinee
della superficie.
Nel caso del cerchio unitario è semplicemente:
|
|
| Per la superficie della sfera
unitaria il procedimento è analogo.
L'equazione cartesiana è: |
x2+y2+z2-1=0 |
quindi del tipo f(x,y,z)=0.
Le equazioni parametriche sono: |
| |
x=cosu·cosv
y=cosu·sinv
z=sinu |
|
dove u è
la latitudine, v la longitudine.
|
Il secondo passaggio fondamentale
è quello di determinare il modo di calcolare le distanze
sulla superficie. |
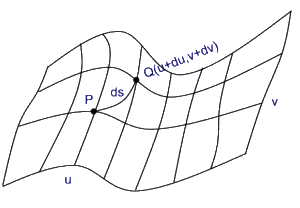 |
Per calcolare la lunghezza di un arco infinitesimale
si serve del teorema di Pitagora
(1) ds2=dx2+dy2+dz2
Dalle equazioni parametriche
x=x(u,v); y=y(u,v);
z=z(u,v),
passando ai differenziali
dx=adu+a'dv; dy=bdu+b'dv;
dz=cdu+c'dv
|
|
Sostituendo nella (1) si
ottiene
|
ds2=Edu2+2Fdudv+Gdv2
|
dove E=a2+b2+c2,
F=aa'+bb'+cc', G=a'2+b'2+c'2,
nota con il nome di prima forma fondamentale.
Questa formula esprime la distanza tra due punti infinitamente
vicini sulla superficie P(u,v) e
Q(u+du,v+dv), da essa, applicando il calcolo
delle variazioni, si possono ottenere le curve di minima distanza
ossia le geodetiche.
Un'altra importante innovazione che Gauss introduce è
la nozione di curvatura di una superficie.
Nel caso delle curve si parte dalla curvatura
di un cerchio, che per definizione si assume come il reciproco
del raggio, cioè K=1/R.
Per determinare la curvatura di una curva in un punto si considera
il cerchio osculatore che è il cerchio
tangente alla curva nel punto P. |
| |
Il cerchio osculatore
si ottiene in questo modo:
si prendono tre punti sulla curva, piuttosto vicini,
P',P,P''; per questi tre punti passa un solo
cerchio;
quindi si fanno avvicinare sempre di più i punti
P' e P'' a P, nella situazione
limite in cui i tre punti coincidono, si ottiene il
cerchio osculatore. La curvatura di questo cerchio è
per definizione la curvatura della curva nel punto P.
|
|
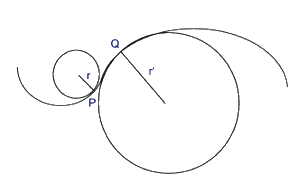 |
La curva rappresentata
ha nei due punti P e Q curvatura di segno opposto.
La curvatura di una retta è nulla. |
|
L'approccio utilizzato per
le curve, tuttavia, non è generalizzabile alle superfici.
Gauss prende spunto da alcune tecniche utilizzate in astronomia.
|
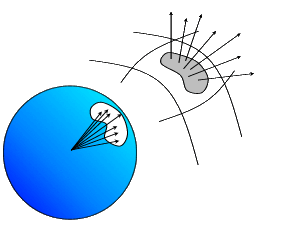 |
La curvatura totale di una porzione limitata
di superficie si definisce attraverso la nozione di normale.
La normale alla superficie in un punto P è la retta
passante da P e perpendicolare al piano tangente alla
superficie condotto dal punto P.
Per definire la curvatura di una superficie, si serve
di una sfera unitaria. Ad ogni punto P della superficie
fa corrispondere un punto P' sulla sfera, in modo che
entrambi abbiano la stessa normale. Se si considera una
piccola regione della superficie contenete P, ad essa
corrisponderà sulla sfera una regione contenente
P'.
La curvatura della superficie in P è definita come
il limite del rapporto tra l'area della regione sulla
sfera e l'area della regione sulla superficie quando queste
due aree tendono a ridursi ai rispettivi punti P e P'.
Gauss ottiene la formula:
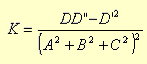 |
|
Dopo numerosi calcoli, Gauss
dimostra una caratteristica particolarmente importante. In
generale, i coefficienti A, B, C, D che compaiono nella formula
della curvatura sembrano dipendere dalle coordinate cartesiane
x,y,z. Se invece la superficie è data per
mezzo di equazioni parametriche, i coefficienti di K
dipendono esclusivamente dalle coordinate curvilinee u
e v.
Da qui un risultato fondamentale per lo studio delle superfici:
la curvatura non dipende dallo spazio circostante,
ma è una caratteristica intrinseca alla superficie
stessa.
In altre parole, si può stabilire se la superficie
è curva o piana restando sulla superficie stessa, senza
fare riferimento a un ipotetico spazio ambiente in cui è
immersa.
Relativamente alla superficie terrestre si può stabilire
il suo grado di curvatura effettuando esclusivamente misure
sulla superficie, senza fare riferimento a osservazioni astronomiche.
|
| In un passo successivo
dimostra che la propria definizione di curvatura corrisponde
a quella data da Eulero e ripresa da Monge. Eulero aveva
proceduto in questo modo: per un punto della superficie
aveva costruito il piano perpendicolare alla superficie
in quel punto. Questo piano determina una curva della
superficie, facendo ruotare il piano si ottengono curve
con differente curvatura. Tra queste ce n'è una
che ha la curvatura minima R1 e
una che ha la curvatura massima R2.
Gauss dimostra che la propria definizione di curvatura,
K, si può ottenere dal prodotto delle
due curvature principali, quella minima e quella massima
K=1/R1·R2. |
|
|
| Questa proprietà ci permette di calcolare
con facilità la curvatura di alcune superfici e di classificarle
in base alla loro curvatura, che può essere positiva,
negativa o nulla.
Gauss ottiene infine un teorema fondamentale per la trattazione
delle superfici, il teorema definito da egli stesso "egregium":
una superficie può essere sovrapposta su un'altra
solo se le due superfici hanno la stessa curvatura.
Questo teorema comporta dei risultati di
particolare importanza. Prima di tutto risolve l'annosa questione
della rappresentazione di una superficie su un altra, in particolare
della rappresentazione della superficie terrestre su una carta
piana. Il teorema dimostra che ciò è impossibile
perché un foglio piano ha curvatura nulla, mentre la
superficie della Terra ha curvatura ovunque positiva. Tuttavia,
nella parte conclusiva delle sue Disquisizioni, Gauss dimostra
che il triangolo terrestre che ha per vertici le colline di
Brocken, Hohehagen e Inselberg si comporta agli effetti pratici
come un triangolo su un foglio piano, poiché l'errore
che si commette è impercettibile.
Ma ancora più importante dal punto di vista teorico
è la conclusione che un pezzo di superficie, per esempio
un triangolo o un'altra figura geometrica, può essere
trasportato da una parte a un'altra della superficie solo
se questa ha in tutti i punti la stessa curvatura, ossia la
curvatura della superficie è costante.
L'importanza di quest'ultima caratteristica
delle superfici è in stretto rapporto con una delle
proprietà fondamentali della geometria, la congruenza
delle figure geometriche che si rileva spostando una figura
su un'altra fino a farle sovrapporre. Se le figure si sovrappongono
perfettamente allora sono uguali. Un'altra conseguenza è
che il concetto stesso di misura si fonda sulla possibilità
di trasportare l'unità di misura da una regione a un'altra
senza che essa si deformi. Le superfici sulle
quali si può costruire una simile geometria sono tutte
quelle a curvatura costante, non solo il piano che ha curvatura
costante nulla ma anche quelle che hanno curvatura costante
positiva o negativa.
|
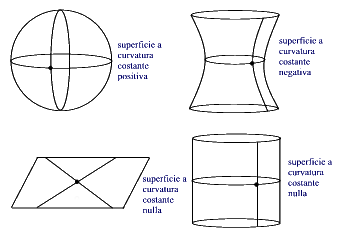 |
La superficie della
sfera ha curvatura costante
positiva, perché in ogni punto le due
curvature principali sono costanti e positive.
La pseudosfera ha curvatura
costante negativa, perché in ogni punto
le due curvature principali sono costanti ma di segno
opposto.
Il piano ha curvatura costante
nulla perché in ogni punto le due curvature
principali sono nulle.
Il cilindro ha curvatura costante nulla, perché
in ogni punto una delle due curvature principali è
sempre nulla. |
|
| Infine, Gauss costruisce i primi elementi della
geometria sulle superfici. Nel piano le costruzioni geometriche
partono dalle rette; sulle superfici non vi sono rette nel senso
comune del termine ma linee geodetiche, le linee della superficie
che uniscono due punti per mezzo del percorso più breve.
Nel piano è un segmento di retta, sulla superficie sferica
è un arco di cerchio massimo, sul cilindro è un
arco di elica.
Quindi, inizia una prima trattazione dei
triangoli geodetici delle superfici. Il primo risultato fondamentale
è che la somma degli angoli interni di un triangolo
geodetico su una superficie curva non è 180°. Lo
scarto rispetto a 180° è dato dall'integrale della
curvatura esteso alla superficie del triangolo.
|
| |
|
Se la curvatura della superficie
è positiva la somma degli angoli interni del
triangolo geodetico supera PIGRECO di una quantità
proporzionale alla sua area; se la curvatura è
negativa la somma degli angoli interni è inferiore
di PIGRECO.
Se la superficie ha curvatura costante, la somma degli
angoli interni del triangolo geodetico differisce da
PIGRECO della quantità KA, dove K è la
curvatura, A è l'area del triangolo. |
|
Tratto da http://www.matematicamente.it
|
| |
 |
 |
|
|