Il test di Friedman

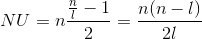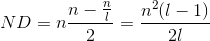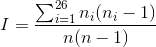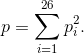
Questo test si basa principalmente su alcuni semplici calcoli di probabilità e sul concetto di indice di coincidenza. Per ogni lingua esistono tabelle con la frequenza di ogni lettera dell’alfabeto, consideriamo ad esempio l’alfabeto inglese e denotiamo con p₁,...,p₂₆la frequenza caratteristica di ogni lettera.
Consideriamo il solito testo cifrato abbastanza lungo, la probabilità che in due posizioni qualsiasi si trovi la lettera di posizione con indice $i$ , è semplicemente $p = p_{i}^{2}$ ; quindi in generale la probabilità che in due posizioni qualsiasi si trovi la stessa lettera è data da

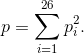
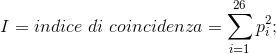
Se consideriamo un testo casuale in cui ogni lettera è equiprobabile cioè p_i=1/26 la probabilità di cui sopra sarà p=0,038, molto inferiore rispetto ad un testo con signiﬁcato in una qualche lingua (ad esempio in italiano questa p=0,075, quasi il doppio).
Si denota con

si osserva che questo indice di coincidenza cresce al crescere dell’irregolarità del testo e diminuisce ﬁno a 0,038 quando tutte le lettere sono equiprobabili, inoltre l’indice è invariante per i cifrari monoalfabetici mentre tende a decrescere per i cifrari polialfabetici.
Ovviamente per un testo cifrato con Vigènere si avrà un indice “più piccolo” rispetto a quello di un cifrario monoalfabetico, che dipenderà dalla lunghezza della chiave e mi permetterà di calcolare quanto vale $l$ =lunghezza chiave.
Un modo analogo per descrivere l’indice di coincidenza è il seguente: supponiamo di avere a disposizione n lettere, di cui n_i è il numero di lettere $i$ -esime, e di volere sapere quale è il numero di coppie possibili formate da lettere uguali; allora questo sarà dato da: .
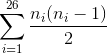Quindi considerando una delle prime deﬁnizioni di probabilità, e cioè il numero di casi possibili fratto il numero di casi favorevoli, ne verrà che la probabilità di scegliere a caso una coppia di lettere uguale è:

E questo per deﬁnizione, coincide con

I

=indice di coincidenza.
Torniamo quindi al metodo per determinare la lunghezza l della chiave: consideriamo una tabella in cui nella colonna i-esima vengono scritte le lettere che occupano il posto i,l + i,2l + i ... (cioè tutte le lettere che sono cifrate con la stessa lettera della parola chiave), uno studio di questo permetterà il calcolo di

I

e conseguentemente di

l

.
Osserviamo che ogni colonna corrisponde ad un cifrario monoalfabetico e quindi la probabilità di trovare una coppia di lettere uguali nella stessa colonna è di 0,075 mentre per colonne diverse scende, supponiamo al minimo e cioè 0,038.
Sia poi

n

il numero di lettere del testo cifrato, allora ogni colonna ha

lettere; scegliamo a caso una lettera tra

n

possibilità, questa mi identiﬁca la colonna di appartenenza in cui avrò

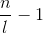modi per scegliere una seconda lettera, cioè il numero di coppie di lettere nella stessa colonna è:

e rispettivamente il numero di coppie che sono in colonne diverse è

Quindi il numero di coppie di lettere uguali è: A=NU*0,075+ND*0,038 e di conseguenza la probabilità (intesa come in precedenza) che una coppia casuale contenga due lettere uguali è

Ma allora poichè per deﬁnizione

P \approx I

e per quanto visto sopra:

ne viene che

Questo numero non sarà sicuramente un intero ma fornirà un ordine di grandezza che mi permetterà di stabilire quale, tra le possibili

l

determinate con metodo di Kasiski è quella esatta; così facendo avrò determinato

l

con una sicurezza piuttosto elevata.