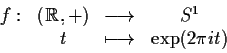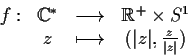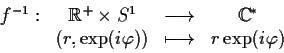Dimostrazione
Sia
![]() un omomorfismo di gruppi continuo in un punto
un omomorfismo di gruppi continuo in un punto ![]() .
Sia
.
Sia ![]() e sia
e sia ![]() un intorno di
un intorno di ![]() .
.
![]() si può scrivere nella forma
si può scrivere nella forma
![]() con
con ![]() intorno di
intorno di ![]() .
Inoltre
.
Inoltre
![]() è un intorno di
è un intorno di ![]() (infatti per continuità in
(infatti per continuità in ![]() ,
esiste
,
esiste ![]() intorno di
intorno di ![]() tale che
tale che
![]() ,
quindi
,
quindi
![]() )
e quindi
)
e quindi
![]() è un intorno di
è un intorno di ![]() .
Essendo
.
Essendo ![]() un omomorfismo di gruppi, ed
essendo
un omomorfismo di gruppi, ed
essendo
![]() ,
si ha poi:
,
si ha poi: