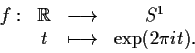Dimostrazione
Sia
![]() l'isomorfismo di gruppi indotto da
l'isomorfismo di gruppi indotto da ![]() .
Proviamo che
.
Proviamo che
![]() è continua e aperta.
è continua e aperta.
Consideriamo il diagramma commutativo
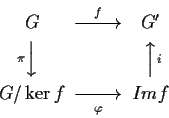
dove
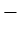
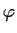 è continua:
è continua:
sia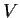 un aperto di
un aperto di
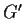 :
:
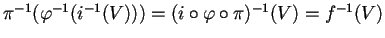 è
aperto essendo
è
aperto essendo 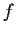 continua, quindi
continua, quindi
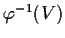 è un aperto di
è un aperto di 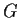 .
.
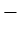
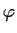 è aperta:
è aperta:
sia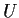 un aperto di
un aperto di 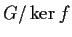 ,
cioè
,
cioè
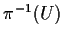 è aperto in
è aperto in 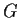 ,
e
,
e
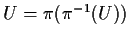 .
Allora
.
Allora
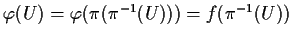 è aperto essendo
è aperto essendo 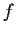 aperta.
aperta.