Proposizione 2
Sia
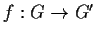
un omomorfismo di gruppi, e siano
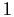
,
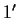
gli elementi neutri rispettivamente di
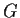
e
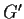
.
Allora:
- 1)
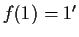 ;
;
- 2)
-
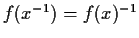 ,
,
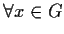 ;
;
- 3)
-
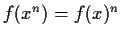 ,
,
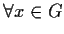 ,
,
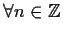 .
.
Dimostrazione
- 1)
-
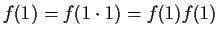 ;
per le
leggi
di cancellazione si ha :
;
per le
leggi
di cancellazione si ha : 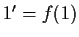 .
.
- 2)
-
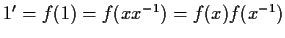 ,
quindi
,
quindi
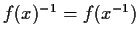 .
.
- 3)
- Supponiamo
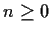 ,
e procediamo per
induzione su
,
e procediamo per
induzione su 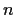 .
.
Se 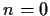 ,
,
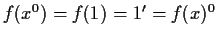 .
.
Supponiamo vero
l'asserto per 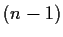 e proviamolo per
e proviamolo per 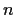 ;
si ha :
;
si ha :
Se invece 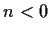 ,
si ha:
,
si ha:
Proposizione 3
Sia
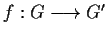 un omomorfismo di gruppi. Allora se
un omomorfismo di gruppi. Allora se 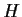 è un sottogruppo di
è un sottogruppo di 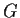 ,
,
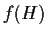 è un sottogruppo di
è un sottogruppo di 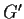 ;
se
;
se
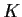 è un sottogruppo di
è un sottogruppo di 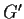 ,
,
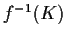 è un sottogruppo di
è un sottogruppo di
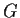 .
.
Dimostrazione
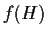 è un sottogruppo di
è un sottogruppo di 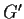 :
:
-
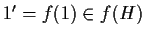 ;
;
- se
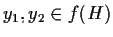 ,
esistono
,
esistono
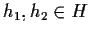 tali che
tali che
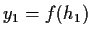 e
e
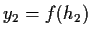 .
Allora
.
Allora
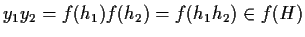 ;
;
- se
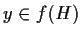 ,
esiste
,
esiste 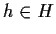 tale che
tale che 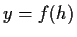 .
Allora
.
Allora
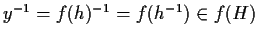 .
.
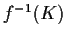
è un sottogruppo di
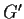
:
-
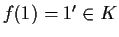 ,
quindi
,
quindi
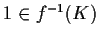 ;
;
- se
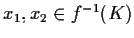 ,
allora
,
allora
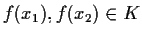 ,
cioè
,
cioè
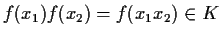 ;
quindi
;
quindi
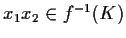 ;
;
- se
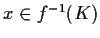 ,
allora
,
allora 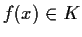 ,
cioè
,
cioè
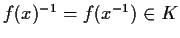 ;
quindi
;
quindi
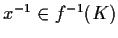 .
.
![]() un omomorfismo di gruppi. Allora se
un omomorfismo di gruppi. Allora se ![]() è un sottogruppo di
è un sottogruppo di ![]() ,
,
![]() è un sottogruppo di
è un sottogruppo di ![]() ;
se
;
se
![]() è un sottogruppo di
è un sottogruppo di ![]() ,
,
![]() è un sottogruppo di
è un sottogruppo di
![]() .
.
![]() è un sottogruppo di
è un sottogruppo di ![]() :
: