- 1)
- Sia
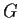 un gruppo. La funzione identità
un gruppo. La funzione identità
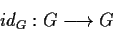
è un omomorfismo. Più in generale, se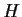 è un sottogruppo di
è un sottogruppo di 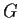 ,
,
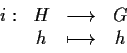
è un omomorfismo iniettivo. - 2)
- Le funzioni
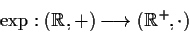
e
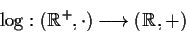
sono omomorfismi di gruppi.- 3)
- Sia
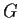 un gruppo e sia
un gruppo e sia 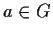 .
La funzione
.
La funzione
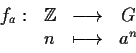
è un omomorfismo dal gruppo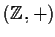 a
a 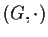 ;
infatti:
;
infatti:
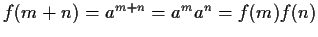 ,
,
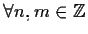 .
.
- 4)
- Sia
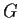 un gruppo abeliano e sia
un gruppo abeliano e sia
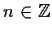 .
La
funzione
.
La
funzione
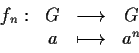
è un omomorfismo; infatti:
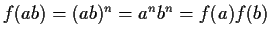 ,
,
 .
.
- 5)
- Sia
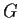 un gruppo e sia
un gruppo e sia 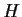 un suo sottogruppo
normale.
un suo sottogruppo
normale.
L'applicazione
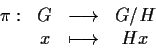
è un omomorfismo suriettivo detto proiezione di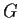 sul quoziente
sul quoziente 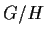 .
.
Verifichiamo che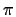 è un omomorfismo:
è un omomorfismo:
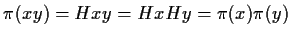 ,
,
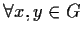 .
.
