Definizione 5   Siano $G$ e $G'$ due gruppi, e sia $f : G \rightarrow G'$ un omomorfismo.
Se $f$ è biunivoca si dice che $f$ è un isomorfismo.
Se $G = G'$, $f$ è detto endomorfismo.
Se $G = G'$ e $f$ è biunivoca, $f$ è un automorfismo.

Proposizione 6   Siano $f : G \rightarrow G'$ e $g: G' \rightarrow G''$ due omomorfismi di gruppi. Allora:
1)
$g \circ f $ è un omomorfismo;
2)
se $f$ è un isomorfismo, anche $f^{-1}$ lo è;
3)
se $f$ e $g$ sono isomorfismi, allora $g \circ f $ è un isomorfismo.
Dimostrazione
1)
Per ogni $x , y \in G$, si ha:

\begin{displaymath}g\circ f(x y) = g(f(xy)) = g(f(x)f(y)) = g(f(x))g(f(y)) = (g\circ f(x))(g\circ f(y))\end{displaymath}

cioè $g \circ f $ è un omomorfismo.
2)
Se $f$ è biunivoca, anche $f^{-1}$ lo è. Inoltre

\begin{displaymath}f(f^{-1}(x) f^{-1}(y)) = (f(f^{-1}(x)))(f(f^{-1}(y))) = xy \end{displaymath}

e applicando $f^{-1}$ a entrambi i membri si ha:

\begin{displaymath}f^{-1}(x)f^{-1}(y) = f^{-1}(xy).\end{displaymath}

3)
L'affermazione segue dal fatto che la composizione di applicazioni biunivoche è biunivoca, e dal punto $1$ di questa proposizione.

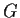
Proposizione 7   L'insieme degli automorfismi di un gruppo $G$, con la composizione, è un gruppo il cui elemento neutro è la funzione identità $id_{G}$.
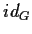
Tale gruppo viene indicato con $Aut(G)$.

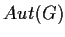
Dimostrazione
L'asserto segue dal fatto che la composizione è associativa e da proposizione 6.

 

previousupnext esercizi