Notazione   Nel seguito $\mathbb{R} $ e $\mathbb{C} $ denoteranno i gruppi $(\mathbb{R} ,+)$ e $(\mathbb{C} ,+)$ rispettivamente, mentre $\mathbb{R} ^{*}$ e $\mathbb{C} ^{*}$ denoteranno i gruppi $(\mathbb{R} ^{*},\cdot)$ e $(\mathbb{C} ^{*},\cdot)$ rispettivamente.

Esercizio 1   Verificare che l'insieme

\begin{displaymath}G=\{(a,b)\in \mathbb{R} ^{2}\vert\,a\neq 0\},\end{displaymath}

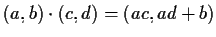
con il prodotto definito da $(a,b)\cdot (c,d)=(ac,ad+b)$, è un gruppo, il cui elemento neutro è $(1,0)$.



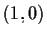
Esercizio 2   Verificare che l'insieme delle affinità della retta reale

\begin{displaymath}Aff(\mathbb{R} )=\{f_{a,b}\vert\,f_{a,b}:\mathbb{R}\longright... ... \mathbb{R} , f_{a,b}(x)=ax+b,\, a,b\in \mathbb{R} , a\neq 0\}\end{displaymath}

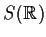
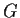
è un sottogruppo di $S(\mathbb{R} )$, isomorfo al gruppo $G$ dell' esercizio 1.


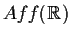
Esercizio 3   Considerare il gruppo $Aff(\mathbb{R} )$ dell'esercizio 2 e provare che:
a)
l'applicazione

\begin{displaymath}\begin{array}{cccc}\varphi:&Aff(\mathbb{R} )&\longrightarrow&\mathbb{R} ^{*}\\ &f_{a,b}&\longmapsto&a\end{array}\end{displaymath}

è l'omomorfismo tra le affinità della retta reale e 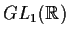$GL_{1}(\mathbb{R} )$ che ad ogni affinità associa la sua parte lineare;
b)
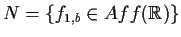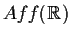l'insieme delle traslazioni della retta reale, $N=\{f_{1,b}\in Aff(\mathbb{R} )\}$, è un sottogruppo normale di $Aff(\mathbb{R} )$;
c)
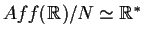$Aff(\mathbb{R} )/N\simeq \mathbb{R} ^{*}$.