5 ESEMPIO
Siano
![$A=[0,1,2],\; B=[-1,0,1],\; P=[0,0,1] \in \mathbf{P^2(R)}.$](img2.gif)
Allora
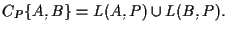
Dato che
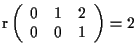
e
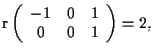
allora equazioni cartesiane per
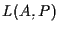
e per
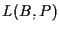
sono (
esempio 14 della sezione "Equazioni di un sottospazio proiettivo"):
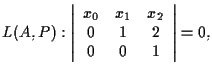
cioè
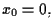
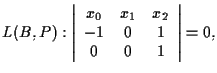
cioè
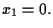
Quindi
![$C_P \{ A,B \} = \{ [x_0,x_1,x_2] \in \mathbf{P^2(R)}:x_0 =0 \} \cup \{ [x_0,x_1...
...n \mathbf{P^2(R)}:x_1 =0
\}=\{ [x_0,x_1,x_2] \in \mathbf{P^2(R)}:x_0 x_1 =0 \}$](img12.gif)
(infatti
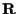
è un campo, quindi il
prodotto
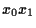
è nullo se e solo se uno dei due fattori è nullo).
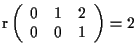 e
e
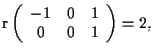 allora equazioni cartesiane per
allora equazioni cartesiane per 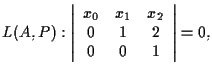 cioè
cioè 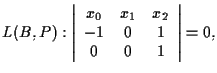 cioè
cioè 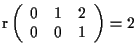 e
e
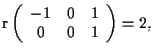 allora equazioni cartesiane per
allora equazioni cartesiane per 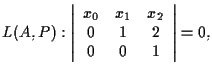 cioè
cioè 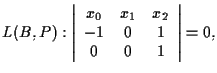 cioè
cioè 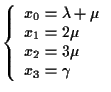 con
con


