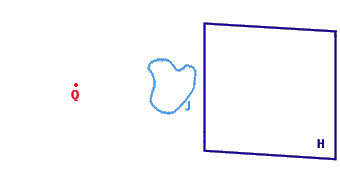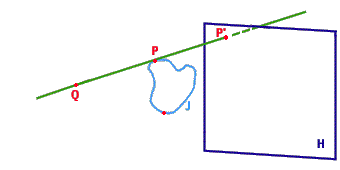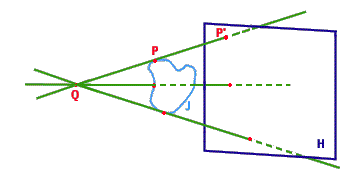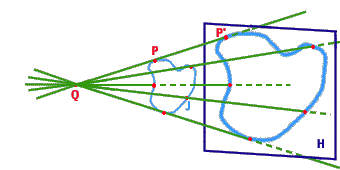
La proiezione di
Notiamo che tale definizione ha senso, perché
![]() quindi
quindi
![]() pertanto (vedi esercizio 8 della sezione "Sottospazi
proiettivi")
pertanto (vedi esercizio 8 della sezione "Sottospazi
proiettivi")
![]() è un punto.
L'applicazione
è un punto.
L'applicazione ![]() è quindi l'applicazione che associa a un punto
è quindi l'applicazione che associa a un punto ![]() il punto di intersezione di
il punto di intersezione di ![]() con la retta congiungente
con la retta congiungente ![]() e
e ![]()