Matrici delle forme hermitiane

Definizione 2.1   Sia $\mathbf{H}$ un $\mathbf{C}$-spazio vettoriale di dimensione finita.
Sia $\mathcal{B}=(\mathbf{v}_{1},\ldots,\mathbf{v}_{n})$ una base per $\mathbf{H}$, sia $h$ una forma hermitiana su $\mathbf{H}$; allora la matrice di $h$ rispetto alla base $\mathcal{B}$ è

\begin{displaymath}Mat(h,\mathcal{B})=(a_{ij}) \end{displaymath}

dove $a_{ij}=h(\mathbf{v}_{i},\mathbf{v}_{j})$.

Dalla definizione di forma hermitiana, si ha che
$a_{ij}=h(\mathbf{v}_{i},\mathbf{v}_{j})=\overline{h(\mathbf{v}_{j},\mathbf{v}_{i})}=\overline{a_{ji}}$
quindi sia $A \in M_{n}(\mathbf{C}), \quad A=(a_{ij}); \quad $ poniamo $\quad \overline{A}=(\overline{a}_{ij})$:
una matrice $H$ è detta hermitiana se $H=\overline{H^{t}}$.
Si noti che se $H$ è una matrice hermitiana, gli elementi sulla sua diagonale principale devono essere reali, poiché devono essere uguali ai loro coniugati, quindi
-
Se $H=(b_{ij})\in M_{n}(\mathbf{C}), \,\, H=\overline{H^{t}} \quad \Rightarrow \quad b_{ii} \in \mathbf{R}$.
-
Inoltre se $A \in M_{n}^{s}(\mathbf{R}) \,$ allora $\, A$, come matrice complessa, è hermitiana.

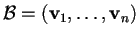
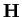
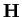
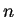
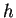
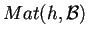
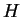
Proposizione 2.2   Sia $\mathcal{B}=(\mathbf{v}_{1},\ldots,\mathbf{v}_{n})$ una base per lo spazio vettoriale $\mathbf{H}$. Esiste una corrispondenza biunivoca fra le forme hermitiane su $\mathbf{H}$ e le matrici hermitiane di ordine $n$; precisamente quella che associa ad una forma hermitiana $h$ la matrice $Mat(h,\mathcal{B})$ e viceversa ad una matrice $H$ hermitiana la forma:
$\qquad h:\mathbf{H} \times \mathbf{H} \rightarrow \mathbf{C}$
$((x_{1},\ldots,x_{n})_{\mathcal{B}},(y_{1},\ldots,y_{n})_{\mathcal{B}}) \rightarrow X^{t}H\overline{Y}$

Dimostrazione