- 1.
-
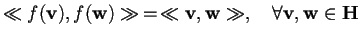 ;
;
- 2.
-
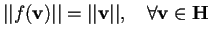 ;
;
- 3.
- se
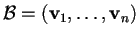 è una base ortonormale allora anche
è una base ortonormale allora anche
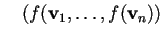 è una base ortonormale.
è una base ortonormale.
- 4.
- esiste una base
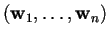 ortonormale tale che
ortonormale tale che
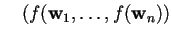 sia una base ortonormale.
sia una base ortonormale.


 Dimostrazione
Allo stesso modo si deduce che
Dimostrazione
Allo stesso modo si deduce che
 Dimostrazione
Come sempre un operatore è associato ad una matrice:
Dimostrazione
Come sempre un operatore è associato ad una matrice:
 Dimostrazione
Dimostrazione
