

- 1.
- Data la base
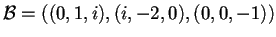 dello spazio hermitiano
dello spazio hermitiano
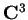 ,
trovare attraverso il procedimento di ortogonalizzazione di Gram-Schimdt, una base ortonormale
,
trovare attraverso il procedimento di ortogonalizzazione di Gram-Schimdt, una base ortonormale
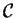 per
per
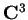 rispetto al prodotto hermitiano standard.
rispetto al prodotto hermitiano standard.
Considerata la base canonica
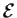 di
di
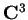 ,
che proprietà ha la matrice
,
che proprietà ha la matrice
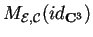 ? Perché?
? Perché?
Vuoi un aiuto?
Per vedere la soluzione totale, clicca  ,
oppure clicca
,
oppure clicca  per visualizzare ogni singolo passo della soluzione.
per visualizzare ogni singolo passo della soluzione.
Allora la base
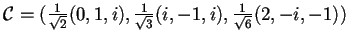 è ortonormale e la matrice di passaggio fra le due basi diventa
è ortonormale e la matrice di passaggio fra le due basi diventa
che è una matrice unitaria, infatti svolgendo i calcoli si può verificare che
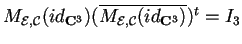 .
.
Gli endomorfismi che portano basi ortonormali in basi ortonormali sono tutti endomorfismi unitari.





dello spazio hermitiano
, trovare attraverso il procedimento di ortogonalizzazione di Gram-Schimdt, una base ortonormale
per
rispetto al prodotto hermitiano standard.
di
, che proprietà ha la matrice
? Perché?
, oppure clicca
per visualizzare ogni singolo passo della soluzione.
è ortonormale e la matrice di passaggio fra le due basi diventa
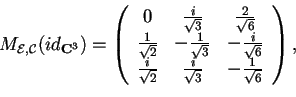
.



 Teoria
Teoria