
Esempi

- 1.
- L'endomorfismo
tale che rispetto alla base canonica
si ha
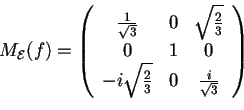
è un endomorfismo unitario, poichéconserva la norma, infatti
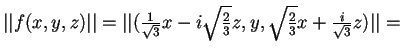
=
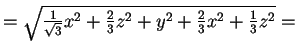
.
- 2.
- La matrice
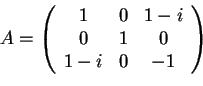
è simmetrica, ma non è unitaria, infatti
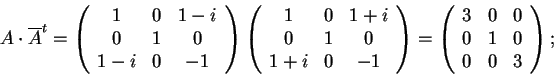
quindi, che implica
.
- 3.
- Si consideri l'endomorfismo unitario
Allora, presa.
, base ortonormale per il prodotto hermitiano standard, abbiamo che
è un'altra base ortonormale per il prodotto hermitiano standard.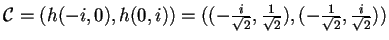


 Teoria
Teoria