
Esercizi

- 1.
- Si consideri
e sia
una base per
. Sia
una forma hermitiana tale che
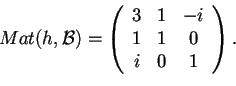
- a)
- Si provi che
è un prodotto hermitiano.
- b)
- Dopo aver trovato una base ortonormale per
partendo da quella assegnata, stabilire se il vettore
è ortogonale al sottospazio
.
- c)
- Si calcoli la proiezione di
su
.
Vuoi un aiuto?
Per vedere la soluzione totale, clicca, oppure clicca
per visualizzare ogni singolo passo della soluzione.
SoluzionePunto b)
- Punto a)
- Per provare che
è una forma definita positiva, basta applicare il criterio dei minori principali e verificare che tutti i minori principali della matrice associata sono positivi:
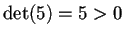
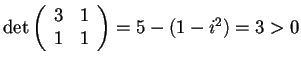
;
alloraè un prodotto hermitiano.
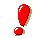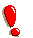
II passo:
- I passo:
- Applichiamo il metodo di ortogonalizzazione di Gram-Schmidt :
iniziamo a normalizzare il primo vettore della base di partenza:
e calcoliamo
;
quindi otteniamoOra calcoliamo gli altri vettori:.
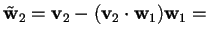
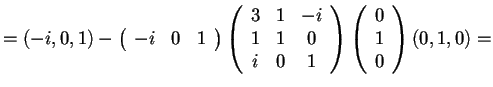
.
Poiché; allora abbiamo
.
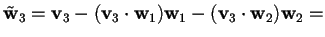
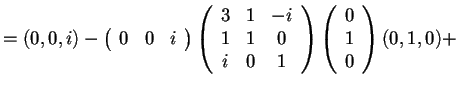
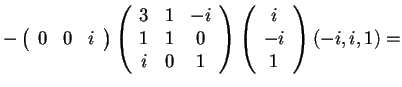
.
Poiché; allora abbiamo
Avremo quindi che.
è una base ortonormale per
.
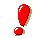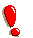
Per semplificare i calcoli, troviamo le coordinate di
Punto c)e dei vettori che generano
rispetto alla nuova base e applichiamo la formula della proiezione ortogonale :
, mentre
.
Ora basta verificare che
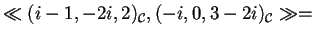
;
ed avremo chenon è ortogonale a
.
- Riportiamo la formula per trovare i coefficienti di Fourier
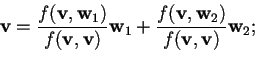
quindi si trova che
,
,
;
allora
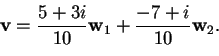



 Teoria
Teoria