Esempi

1.
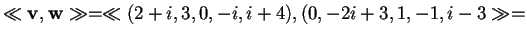
Consideriamo $\mathbf{H}=\mathbf{C}^5$ con il prodotto hermitiano standard e la base canonica $\mathcal{E}$, allora il prodotto fra i due vettori $\mathbf{v}=(2+i,3,0,-i,i+4)$ e $\mathbf{w}=(0,2i+3,1,-1,i-3)$ sarà: $\ll \mathbf{v}, \mathbf{w} \gg=\ll (2+i,3,0,-i,i+4),(0,-2i+3,1,-1,i-3 \gg=$
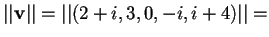
$= 3(3+2i)-i+(i+4)(i-3)=-4+4i$ mentre la norma del primo vettore sarà: $\vert\vert\mathbf{v}\vert\vert=\vert\vert(2+i,3,0,-i,i+4)\vert\vert=$
$=\sqrt{(2+i)(2-i)+9+(-i)i+(i-4)(-4-i)}=\sqrt{22}$.

2.
Sia $\mathbf{H}=\mathcal{C}^3$ e sia $h$ un prodotto hermitiano tale che rispetto alla base canonica risulta

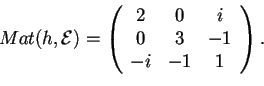
\begin{displaymath}Mat(h,\mathcal{E})= \begin{array}({ccc}) 2 & 0 & i\\ 0 & 3 & -1\\ -i & -1 & 1 \end{array}. \end{displaymath}

Vogliamo provare che i sottospazi $\mathbf{U}$ e $\mathbf{W}$ definiti come
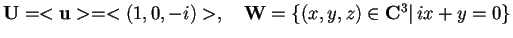
$\mathbf{U}=<\mathbf{u}>=<(1,0,-i)>, \quad \mathbf{W}=\{ (x,y,z)\in \mathbf{C}^3 \vert \, ix+y=0 \}$
sono ortogonali.
Svolgendo i calcoli, si trova che
$\mathbf{W}=\{ (x,-ix,z)\in\mathbf{C}^3 \vert \, x,z \in \mathbf{C} \}$, allora
$\mathbf{W}=<\mathbf{w}_{1},\mathbf{w}_{2}>=<(1,-i,0),(0,0,1)>$;
quindi dobbiamo verificare che siano nulli i prodotti hermitiani fra i vettori che generano $\mathbf{W}$ e $\mathbf{U}$. Infatti
$\ll \mathbf{u},\mathbf{w}_{1}\gg= \begin{array}({ccc}) 1 & 0 & -i \end{array... ... -i & -1 & 1 \end{array} \begin{array}({c}) 1\\ i\\ 0 \end{array} =0$,
$\ll \mathbf{u},\mathbf{w}_{2}\gg= \begin{array}({ccc}) 1 & 0 & -i \end{array... ... -i & -1 & 1 \end{array} \begin{array}({c}) 0\\ 0\\ -1 \end{array} =0$.