Teorema spettrale

$\qquad$ Finora abbiamo analizzato due diverse relazioni di equivalenza in $M_{n}(K)$ :

-: la similitudine: $\qquad A,B \in M_{n}(K), \,\, \exists M \in GL_{n}(K) : B=M^{-1}AM$ ;
-: la congruenza: $\,\, \qquad A,B \in M_{n}(K), \,\, \exists M \in GL_{n}(K) : B=M^{t}AM$ .

Lo studio era finalizzato a determinare, rispetto a due basi diverse, le matrici associate nel primo caso allo stesso operatore in uno spazio vettoriale, nel secondo alla stessa forma bilineare.
Entrambe le classi di problemi avevano lo scopo di trovare una matrice diagonale equivalente a quella data, ma, mentre per la similitudine l'esistenza della soluzione non sempre è ammessa, per la congruenza, invece, se restringiamo il campo alle sole forme simmetriche, possiamo sempre trovare una base diagonalizzante.
Ora vogliamo studiare una relazione più "forte": restringiamo la nostra attenzione alle matrici simmetriche reali e considereremo le matrici che si ottengono da queste attraverso matrici ortogonali, cioè data $A \in M_{n}^{s}(\mathbf{R})$ , le matrici del tipo $M^{t}AM$ , ove $M \in O(n)$ .
In questo caso avremo:

$M^{-1}AM=M^{t}AM$ ,

quindi senza più distinzione fra similitudine e congruenza.
Pertanto se prendiamo in considerazione solo matrici

che esprimono il cambiamento di base fra basi ortonormali in uno spazio vettoriale euclideo di dimensione

, le due nozioni diventano equivalenti. Questa preambolo introduce al seguente, fondamentale, teorema:

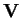
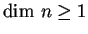
Teorema 9.1 (Teorema Spettrale Reale) Sia $\mathbf{V}$ uno spazio vettoriale euclideo di $\dim \, n \geq 1$ .
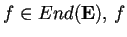
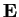
Sia $f \in End(\mathbf{E}), \, f$ simmetrico; allora esiste una base ortonormale di $\mathbf{E}$ composta da autovettori per

Dimostrazione

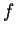
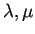
Corollario 9.3 Nelle ipotesi del teorema precedente, se $\lambda, \mu$ sono autovalori distinti per

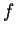
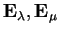
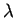
, allora $\mathbf{E}_{\lambda},\mathbf{E}_{\mu}$ sono ortogonali, cioè ogni autovettore relativo a $\lambda$ è ortogonale ad ogni autovettore relativo a $\mu$ .

Dimostrazione

Proposizione 9.4 Sono forme equivalenti al teorema spettrale i seguenti enunciati:

1.: $A \in M_{n}^{s}(\mathbf{R}) \, \Rightarrow \quad \exists$ una matrice $M \in O(n)$ tale che
$M^{-1}AM=M^{t}AM$ è diagonale.
2.: Se $f \in Bils(\mathbf{E})$ , con $\mathbf{E}$ spazio vettoriale euclideo di dimensione $n \geq 1$ .
Allora esiste una base ortonormale di $\mathbf{E}$ diagonalizzante per .

Dimostrazione

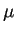
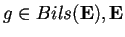
Osservazione 9.5 Sia $g \in Bils(\mathbf{E}), \mathbf{E}$ spazio vettoriale euclideo.
Per calcolare la segnatura di

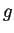
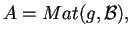
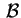
basta considerare $A=Mat(g,\mathcal{B}), \,$ ove $\, \mathcal{B}$ è una base qualsialsi e poi calcolare gli autovalori di

.
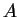
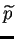
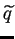
Sia $\widetilde{p}$ il numero di autovalori positivi e $\widetilde{q}$ il numero di quelli negativi (entrambi contati con le loro molteplicità).
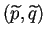
Allora $(\widetilde{p},\widetilde{q})$ è la segnatura di

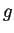
; infatti rispetto ad una base ortonormale di autovettori (che esiste per il teorema (9.1)),

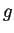
verrà espressa da una matrice diagonale avente gli autovettori sulla diagonale.

Questi nuovi risultati trovano le loro principali applicazioni geometriche nella classificazione delle quadriche (in particolare, in $\mathbf{R}^2$ , delle coniche), negli spazi euclidei.