

- 1.
- Data la matrice
che rappresenta la forma bilineare simmetrica  rispetto alla base canonica di
rispetto alla base canonica di
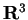 ,
,
- a)
- trovare una base ortonormale di autovettori per
 .
.
- b)
- la matrice è ortogonalmente simile a
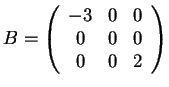 ?
?
Se sì , calcolare la matrice 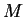 tale che
tale che
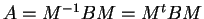 .
.
- c)
- Verificare che gli autospazi relativi agli autovettori sono fra loro ortogonali.
Vuoi un aiuto?
Per vedere la soluzione totale, clicca  ,
oppure clicca
,
oppure clicca  per visualizzare ogni singolo passo della soluzione.
per visualizzare ogni singolo passo della soluzione.
Soluzione
- Punto a)
- Applichiamo il procedimento base visto negli esempi (9.1):
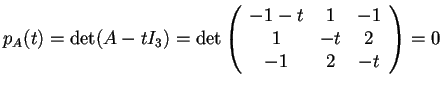
che dà l'equazione
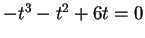 ,
i cui zeri sono
,
i cui zeri sono
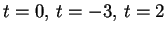 .
.
Quindi  ha tre autovalori distinti:
che hanno tutti molteplicità algebrica 1.
ha tre autovalori distinti:
che hanno tutti molteplicità algebrica 1.
Calcoliamo gli autospazi relativi:
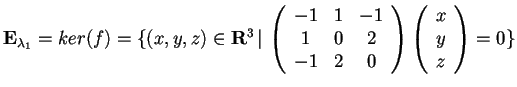 ,
,
da cui:
che ha soluzione per
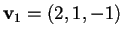 ;
quindi
;
quindi
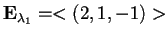 ,
e, normalizzando il vettore, otteniamo una base ortonormale per il sottospazio ortogonale:
,
e, normalizzando il vettore, otteniamo una base ortonormale per il sottospazio ortogonale:
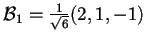 .
.
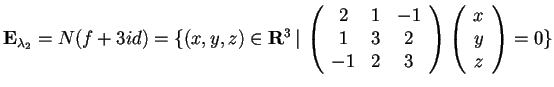 ,
,
da cui:
che ha soluzione per
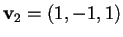 ;
quindi
;
quindi
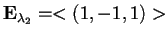 ,
e, normalizzando il vettore, la base ortonormale per il sottospazio ortogonale:
,
e, normalizzando il vettore, la base ortonormale per il sottospazio ortogonale:
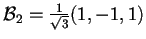 .
.
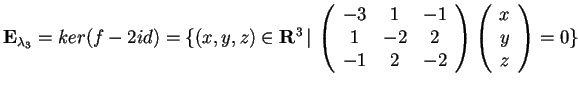 ,
,
da cui otteniamo:
che ha soluzione per
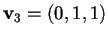 ;
quindi
;
quindi
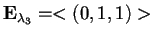 ,
e, normalizzando il vettore, otteniamo ancora una base ortonormale:
,
e, normalizzando il vettore, otteniamo ancora una base ortonormale:
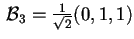 .
.
Quindi una base ortonormale per  è:
è:
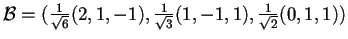
.
Punto
b) 
- I passo:
- Siccome gli autovalori di
 sono 0,-3,2, avremo che
sono 0,-3,2, avremo che
ove
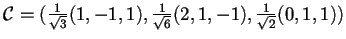 ;
;
quindi le due matrici sono ortogonalmente simili.
II passo:

La matrice 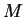 cercata sarà data dalla matrice del cambiamento di base da
cercata sarà data dalla matrice del cambiamento di base da
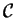 a
a
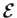 ,
che si ottiene così
da cui abbiamo
,
che si ottiene così
da cui abbiamo
Punto
c) 
-
- Dobbiamo verificare che siano ortogonali rispetto
 :
:
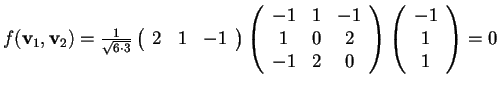 ,
,
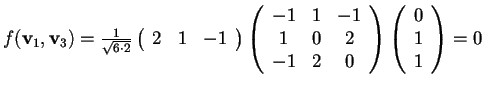 ,
,
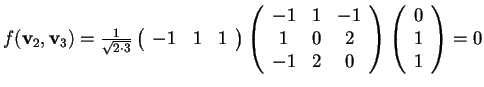 .
.





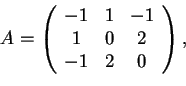
rispetto alla base canonica di
,
.
?
tale che
.
, oppure clicca
per visualizzare ogni singolo passo della soluzione.
Soluzione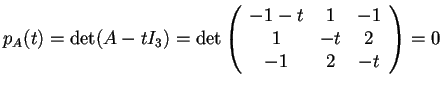
, i cui zeri sono
.
ha tre autovalori distinti:
che hanno tutti molteplicità algebrica 1.,
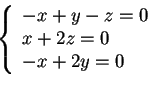
; quindi
, e, normalizzando il vettore, otteniamo una base ortonormale per il sottospazio ortogonale:
.
,
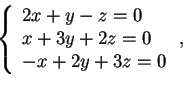
; quindi
, e, normalizzando il vettore, la base ortonormale per il sottospazio ortogonale:
.
,
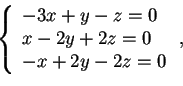
; quindi
, e, normalizzando il vettore, otteniamo ancora una base ortonormale:
.
è:
.

sono 0,-3,2, avremo che
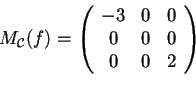
;

cercata sarà data dalla matrice del cambiamento di base da
a
, che si ottiene così
da cui abbiamo,
,
,
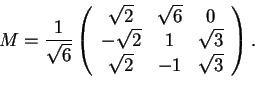

:
,
,
.



 Teoria
Teoria