
 Data la matrice associata alla forma bilineare simmetrica
Data la matrice associata alla forma bilineare simmetrica 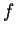 sullo spazio vettoriale euclideo
sullo spazio vettoriale euclideo
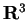 (rispetto alla base canonica):
(rispetto alla base canonica):
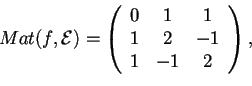
vogliamo trovare una base ortonormale di
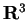 di autovettori per
di autovettori per 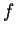 .
.
Enunciamo di seguito il procedimento base, che risulterà molto utile per svolgere esercizi:
- I passo:
- Calcolare gli zeri
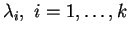 del polinomio caratteristico della matrice col le loro rispettive molteplicità
del polinomio caratteristico della matrice col le loro rispettive molteplicità
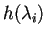 ,
che risulteranno tali che
,
che risulteranno tali che
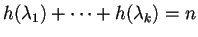 dimensione dello spazio euclideo.
dimensione dello spazio euclideo.
- II passo:
- Per ogni valore
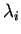 ,
determinare una base per l'autospazio
,
determinare una base per l'autospazio
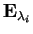 .
.
- III passo:
- Ortonormalizzare la base di
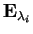 .
.
- IV passo:
- Costruire una base ortonormale
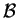 di
di
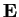 formata dalle basi ortonormali dei sottospazi
formata dalle basi ortonormali dei sottospazi
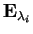 ;
risulterà che la matrice del canbiamento di base
;
risulterà che la matrice del canbiamento di base
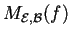 è ortogonale, mentre
è ortogonale, mentre
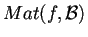 è una matrice diagonale la cui diagonale principale è formata dall'autovalore
è una matrice diagonale la cui diagonale principale è formata dall'autovalore
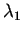 per
per
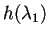 volte, da
volte, da
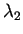 per
per
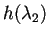 volte, fino a
volte, fino a
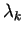 per
per
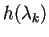 volte.
volte.
Applichiamo questo procedimento alla matrice data:
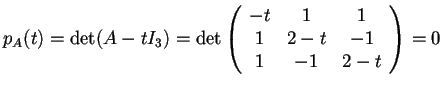
da cui, svolgendo i calcoli, si ottiene l'equazione
che ha soluzioni:
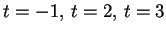 .
.
Gli autovalori
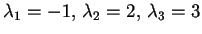 hanno tutti molteplicità algebrica 1; quindi calcoliamo i sottospazi ortogonali relativi:
hanno tutti molteplicità algebrica 1; quindi calcoliamo i sottospazi ortogonali relativi:
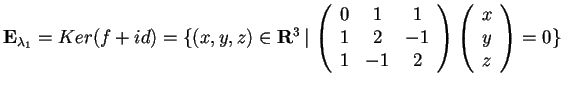 .
.
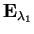 è dato dalle soluzioni del sistema
è dato dalle soluzioni del sistema
le cui soluzioni sono generate da
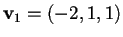 ;
quindi
;
quindi
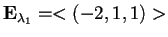 ,
e, normalizzando il vettore, otteniamo una base ortonormale per il sottospazio ortogonale:
,
e, normalizzando il vettore, otteniamo una base ortonormale per il sottospazio ortogonale:
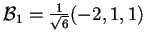 .
.
Procediamo analogamente per gli altri due sottospazi:
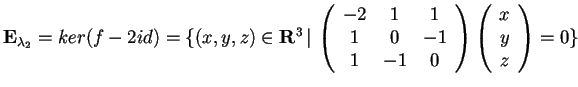 ,
,
che ci dà:
di soluzione
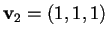 ;
quindi
;
quindi
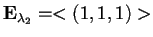 ,
e, normalizzando il vettore, la base ortonormale per il sottospazio ortogonale:
,
e, normalizzando il vettore, la base ortonormale per il sottospazio ortogonale:
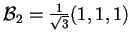 .
.
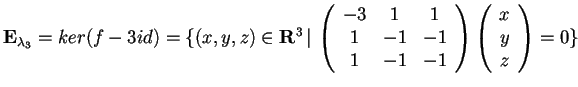
da cui:
che ha per soluzione:
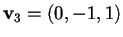 ;
quindi
;
quindi
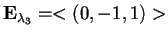 ,
e, normalizzando il vettore, otteniamo ancora una base ortonormale:
,
e, normalizzando il vettore, otteniamo ancora una base ortonormale:
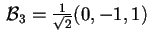 .
.
La matrice del cambiamento di base
è ortogonale, infatti



Data la matrice associata alla forma bilineare simmetrica
sullo spazio vettoriale euclideo
(rispetto alla base canonica):
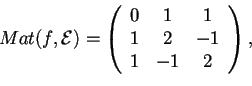
di autovettori per
.
del polinomio caratteristico della matrice col le loro rispettive molteplicità
, che risulteranno tali che
dimensione dello spazio euclideo.
, determinare una base per l'autospazio
.
.
di
formata dalle basi ortonormali dei sottospazi
; risulterà che la matrice del canbiamento di base
è ortogonale, mentre
è una matrice diagonale la cui diagonale principale è formata dall'autovalore
per
volte, da
per
volte, fino a
per
volte.
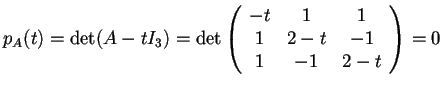
.
hanno tutti molteplicità algebrica 1; quindi calcoliamo i sottospazi ortogonali relativi:
.
è dato dalle soluzioni del sistema
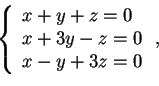
; quindi
, e, normalizzando il vettore, otteniamo una base ortonormale per il sottospazio ortogonale:
.
,
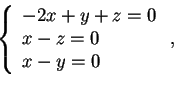
; quindi
, e, normalizzando il vettore, la base ortonormale per il sottospazio ortogonale:
.
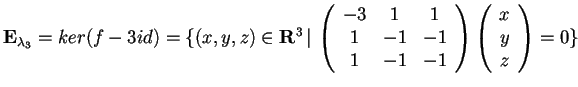
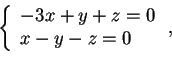
; quindi
, e, normalizzando il vettore, otteniamo ancora una base ortonormale:
.
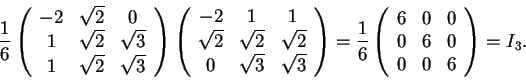

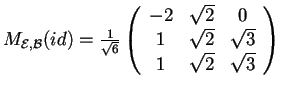

 Teoria
Teoria