Classificazione degli endomorfismi

$\qquad$ Abbiamo visto che se $f$ è un endomorfismo unitario e $f(\mathbf{v})=0$, allora $\mathbf{v}=0$; questo implica che il nucleo dell'applicazione è il sottospazio generato dal vettore nullo, cioè $ker(f)=<0>$, e quindi che l'operatore unitario è invertibile.
Da ciò si ricava facilmente che gli operatori unitari formano un sottogruppo:

Definizione 7.1   L'insieme

\begin{displaymath}O(\mathbf{E}):= \lbrace f \in GL(\mathbf{E}) \, \vert \, f \, \textrm{ unitario } \, \rbrace \end{displaymath}

è un sottogruppo di $(GL(\mathbf{E}),\cdot)$, detto il gruppo ortogonale di $\mathbf{E}$.

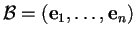
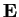
Proposizione 7.2   Sia $\mathcal{B}=(\mathbf{e}_{1},\ldots,\mathbf{e}_{n})$ base ortonormale di $\mathbf{E}$; allora
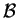
il prodotto scalare di due vettori espressi rispetto a $\mathcal{B}$ è uguale al prodotto scalare standard dei vettori delle loro coordinate, quindi l'isomorfismo di gruppo:
$\phi_{\mathcal{B}}:(GL(\mathbf{E}),\cdot) \rightarrow (GL_{n}(\mathbf{R}),\cdot)$
$f \rightarrow M_{\mathcal{B}}(f)$
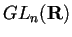
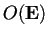
ove il prodotto in $GL_{n}(\mathbf{R})$ è l'usuale prodotto righe per colonne, induce un isomorfismo tra i sottogruppi $O(\mathbf{E})$ e $O(n)$.

Dimostrazione

Una caratteristica delle matrici ortogonali è la seguente:
$A \in O(n) \quad \Rightarrow \quad \det(A)= \pm 1$.
Infatti $A^{t}=A^{-1}$, quindi $\det (A)=\det(A^{t})=\det(A^{-1})=\frac{1}{\det(A)}$, cosicché:
$(\det(A))^{2}=1 \quad \Rightarrow \quad \det(A)= \pm 1$ .
Se il segno di $A$ è positivo, si definisce

\begin{displaymath}SO(n):= \lbrace A \in O(n) \, \vert \, \det(A)=1 \rbrace, \end{displaymath}

che è un sottogruppo di $O(n)$ detto il gruppo ortogonale speciale di ordine n, (mentre $SO^{-}(n)=\lbrace A \in O(n) \, \vert \, \det(A)=-1 \rbrace$ non è un sottogruppo, perché non è chiuso rispetto al prodotto).
Se $f \in O(\mathbf{E}) \,$ allora $\, \det f= \pm 1, \, $ pertanto l'isomorfismo $\phi_{\mathcal{B}}$ induce una corrispondenza biunivoca fra il sottogruppo $SO(n) \subset O(n) \,$ e $\, SO(\mathbf{E}) \subset O(\mathbf{E})$, definito come:

\begin{displaymath}SO(\mathbf{E}):= \lbrace f \in O(\mathbf{E}) \, \vert \, \det(f)=1 \rbrace, \end{displaymath}

che è un sottogruppo di $O(\mathbf{E})$ detto il gruppo ortogonale speciale di ordine n.
Allora, data una base ortonormale $\mathcal{B}$, avremo:
$ f \in SO(\mathbf{E}) \quad \Longleftrightarrow \quad M_{\mathcal{B}}(f) \in SO(n).$
Gli elementi di $SO(\mathbf{E})$ sono detti rotazioni di $\mathbf{E}$, mentre tra gli elementi di $SO^{-}(n)$ ci sono particolari isometrie negative chiamate riflessioni.
Arriviamo quindi ad un importante risultato:

Proposizione 7.3   Sia $f \in O(\mathbf{E})$; se $\lambda $ è un autovalore per $f$, avremo $\lambda = \pm 1$.
Equivalentemente, se $A \in O(n)$ e $\lambda $ è un autovalore per $A,\quad \lambda = \pm 1$).

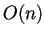
Dimostrazione