- 1.
-
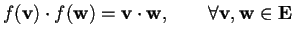 ;
;
cioè conserva il prodotto scalare;
conserva il prodotto scalare;
- 2.
-
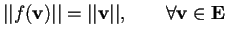 ;
;
cioè conserva la norma;
conserva la norma;
- 3.
- se
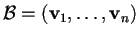 è una base ortonormale per
è una base ortonormale per
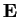 ,
allora
,
allora
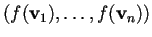 è una base ortonormale per
è una base ortonormale per
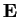 .
.
Quindi in particolare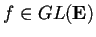 .
.
- 4.
- esiste una base ortonormale
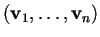 tale che
tale che
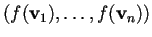 sia una base ortonormale per
sia una base ortonormale per
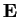 .
.

 Dimostrazione
Un operatore unitario
Dimostrazione
Un operatore unitario 

 Esempi
Esempi Esercizi
Esercizi