
Esercizi
Quale dei seguenti endomorfismi è unitario?
In ciascun caso, giustificare la risposta.
- a)
;
- b)
;
- c)
.
Vuoi un aiuto?
Per vedere la soluzione totale, clicca, oppure clicca
per visualizzare ogni singolo passo della soluzione.
Punto c)
- L'endomorfismo non è unitario perché
non conserva il prodotto scalare, infatti, presi i vettori della base canonica:
,
mentre.

- L'endomorfismo non è unitario perché non è lineare, infatti
.

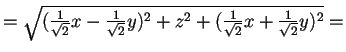
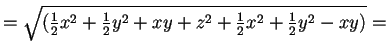

 Teoria
Teoria