Esempi

1.
Sia data la base canonica $\mathcal{E}$ su $\mathbf{R}^2$ con il prodotto scalare standard e l'endomorfismo $f:\mathbf{R}^2\rightarrow\mathbf{R}^2$ definito da:
$f(\mathbf{e}_{1})=3\mathbf{e}_{1}+2\mathbf{e}_{2}$
$f(\mathbf{e}_{2})=\mathbf{e}_{1}+\mathbf{e}_{2}$.
Allora l'endomorfismo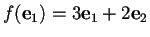 $f$ non è unitario perché non conserva il prodotto scalare, infatti
$f((1,0))\cdot f((0,1))=(3,2)\cdot (1,1)=3+2=5$,
mentre $(0,1)\cdot (0,1)=0$.

2.
L'endomorfismo $g:\mathbf{R}^3 \rightarrow\mathbf{R}^3$ tale che
$g(x,y,z)=(\frac{1}{2}x-\frac{\sqrt{3}}{2}y,\frac{\sqrt{3}}{2}x+\frac{1}{2}y,z)$
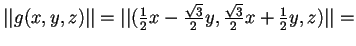
è unitario perché conserva la norma su $\mathbf{R}^3$, infatti, preso il prodotto scalare standard, si ha: $\vert\vert g(x,y,z)\vert\vert=\vert\vert(\frac{1}{2}x-\frac{\sqrt{3}}{2}y,\frac{\sqrt{3}}{2}x+\frac{1}{2}y,z)\vert\vert=$
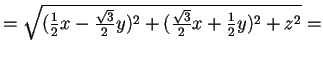
$=\sqrt{(\frac{1}{2}x-\frac{\sqrt{3}}{2}y)^2+(\frac{\sqrt{3}}{2}x+\frac{1}{2}y)^2+z^2}=$
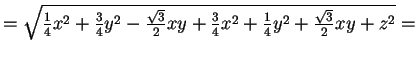
$=\sqrt{\frac{1}{4}x^2+\frac{3}{4}y^2-\frac{\sqrt{3}}{2}xy+\frac{3}{4}x^2+\frac{1}{4}y^2+\frac{\sqrt{3}}{2}xy+z^2}=$
$=\sqrt{x^2+y^2+z^2}=\vert\vert(x,y,z)\vert\vert$.