Esempi

1.
Riconsideriamo gli endomorfismi unitari incontrati negli esempi (6.1) e negli esercizi (6.2):
$f:\mathbf{R}^2\rightarrow\mathbf{R}^2, \quad f(x,y)=(\frac{1}{2}x-\frac{\sqrt{3}}{2}y,\frac{\sqrt{3}}{2}x+\frac{1}{2}y)$
è tale che

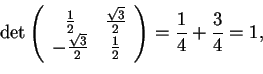
\begin{displaymath}\det \begin{array}({cc}) \frac{1}{2} & \frac{\sqrt{3}}{2}\\... ...}}{2} & \frac{1}{2} \end{array} =\frac{1}{4}+\frac{3}{4}=1, \end{displaymath}

quindi appartiene al gruppo ortogonale speciale di ordine 3, mentre per
$f:\mathbf{R}^3 \rightarrow\mathbf{R}^3, \quad f(x,y,z)=(\frac{1}{\sqrt{2}}x-\frac{1}{\sqrt{2}}y,z,\frac{1}{\sqrt{2}}x+\frac{1}{\sqrt{2}}y)$
si ha che

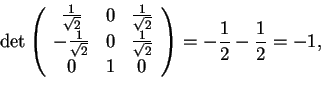
\begin{displaymath}\det \begin{array}({ccc}) \frac{1}{\sqrt{2}} & 0 & \frac{1}... ...2}}\\ 0 & 1 & 0 \end{array} =-\frac{1}{2}-\frac{1}{2}=-1, \end{displaymath}

perciò appartiene a $SO^{-}(3)$.

2.
La matrice più rappresentativa di $SO(2)$ è quella delle rotazioni in $\mathbf{R}^2$, cioè:

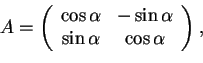
\begin{displaymath}A= \begin{array}({cc}) \cos \alpha & - \sin\alpha \\ \sin \alpha & \cos \alpha \end{array}, \end{displaymath}

mentre per le riflessioni in $\mathbf{R}^2$ si usa:

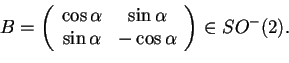
\begin{displaymath}B= \begin{array}({cc}) \cos \alpha & \sin \alpha \\ \sin \alpha & - \cos \alpha \end{array} \in SO^{-}(2). \end{displaymath}