

- 1.
- Data la matrice
- a)
- può essere la matrice di un endomorfismo unitario?
Se sì , negativo o positivo?
- b)
- Se prendiamo
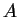 come la matrice del prodotto scalare standard "
come la matrice del prodotto scalare standard "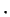 " rispetto ad una base ortonormale, la matrice
" rispetto ad una base ortonormale, la matrice
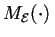 con
con
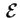 base canonica, è ancora la matrice di una isometria?
base canonica, è ancora la matrice di una isometria?
Vuoi un aiuto?
Per vedere la soluzione totale, clicca  ,
oppure clicca
,
oppure clicca  per visualizzare ogni singolo passo della soluzione.
per visualizzare ogni singolo passo della soluzione.
-
- Sì , perché l'insieme delle matrici ortogonali
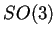 è un sottospazio vettoriale (perciò chiuso rispetto alla moltiplicazione), quindi il prodotto di matrici ortogonali è ortogonali.
è un sottospazio vettoriale (perciò chiuso rispetto alla moltiplicazione), quindi il prodotto di matrici ortogonali è ortogonali.





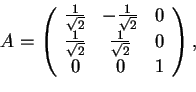
come la matrice del prodotto scalare standard "
" rispetto ad una base ortonormale, la matrice
con
base canonica, è ancora la matrice di una isometria?
, oppure clicca
per visualizzare ogni singolo passo della soluzione.
Soluzionee
, possiamo dire che
è la matrice di un endomorfismo unitario se è ortogonale, quindi si ha che
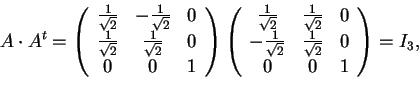
è la matrice di un endomorfismo unitario.
, quindi
.

è un sottospazio vettoriale (perciò chiuso rispetto alla moltiplicazione), quindi il prodotto di matrici ortogonali è ortogonali.



 Teoria
Teoria