Teorema 2.1
Sia
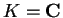
e sia
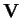
un
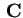
-spazio vettoriale,
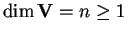
e
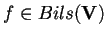
.
Allora esiste una base diagonalizzante
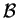
per
tale che nella notazione a blocchi risulta:
dove
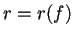
.
Equivalentemente ogni matrice
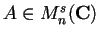
è congruente ad una matrice di questo tipo, con
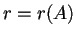
.
Teorema 2.2 (di Sylvester)
Sia
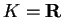
e sia
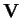
un
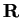
-spazio vettoriale,
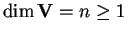
e
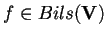
e
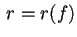
.
Allora esiste un intero non negativo
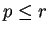
che dipende solo da
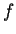
e una base diagonalizzante
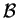
per
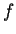
tale che nella notazione a blocchi risulta:
Equivalentemente ogni matrice
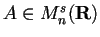
è congruente a una matrice di questo tipo con
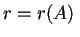
e
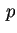
che dipende solo da
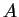
.
Definizione 2.3
Sia
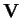
un
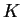
-spazio vettoriale di dimensione finita
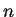
,
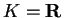
o
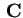
.
Sia
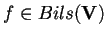
e sia
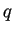
la forma quadratica associata a
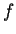
.
Sia
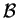
una base come nel primo teorema di Sylvester se
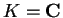
e come nel secondo teorema di Sylvester se
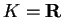
.
Allora si ha ponendo
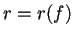
:
se
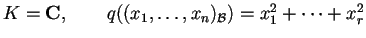
;
se
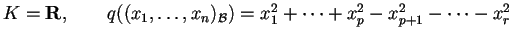
.
Questa espressione è detta
forma canonica della forma quadratica complessa (risp. reale)
.
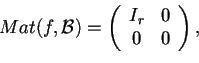


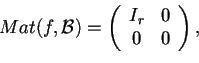
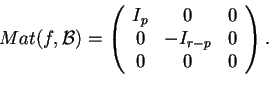
 Dimostrazione dei due teoremi
Dimostrazione dei due teoremi
