

- 1.
- Determinare la forma canonica sia in
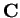 che in
che in
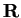 delle seguenti forme quadratiche su
delle seguenti forme quadratiche su
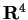 :
:
- a)
-
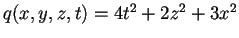 ,
,
- b)
-
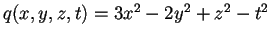 ,
,
- c)
-
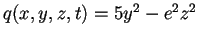 .
.
Vuoi un aiuto?
Per vedere la soluzione totale, clicca  ,
oppure clicca
,
oppure clicca  per visualizzare ogni singolo passo della soluzione.
per visualizzare ogni singolo passo della soluzione.
Soluzione
-
- Punto a)
- La matrice associata è:
quindi per il teorema di Sylvester, esiste una base diagonalizzante tale che nella notazione a blocchi la matrice sia congruente ad una matrice 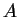 diagonale del tipo:
diagonale del tipo:
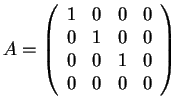
;
pertanto la sua forma canonica sarà:
in
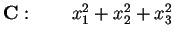
;
in
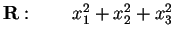
.
Punto
b)
-
- La matrice è congruente ad una matrice diagonale del tipo:
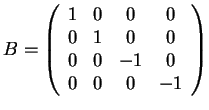
,
quindi la forma canonica diventa
in
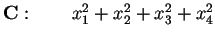
;
in
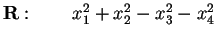
.
Punto
c)
-
- La matrice è congruente ad una matrice diagonale del tipo:
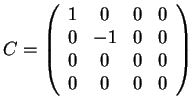
,
quindi la forma canonica risulta
in
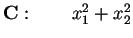
;
in
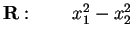
.





che in
delle seguenti forme quadratiche su
:
,
,
.
, oppure clicca
per visualizzare ogni singolo passo della soluzione.
Soluzione
diagonale del tipo:
;
;
.
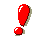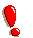
,
in;
.
,
in;
.



 Teoria
Teoria