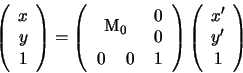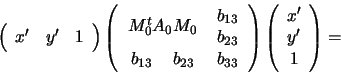PASSO I
Il teorema spettrale
ci assicura, che data una matrice 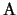 simmetrica reale, che definisce sia una forma quadratica che un
endomorfismo diagonalizzabile, esiste una matrice ortogonale
simmetrica reale, che definisce sia una forma quadratica che un
endomorfismo diagonalizzabile, esiste una matrice ortogonale 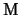 tale che
tale che
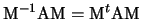 è diagonale. Quindi è possibile trovare una
matrice
è diagonale. Quindi è possibile trovare una
matrice 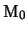 ortogonale tale che la trasformazione
lineare:
ortogonale tale che la trasformazione
lineare:
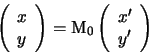 |
(9) |
riduca la forma quadratica (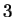 ) nella forma
) nella forma
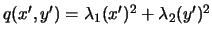 dove
dove 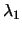 e
e
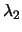 non sono simultaneamente nulli. La matrice associata
alla forma è
non sono simultaneamente nulli. La matrice associata
alla forma è
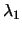 e
e 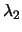 autovalori di
autovalori di 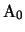 .
Secondo quanto visto in (
.
Secondo quanto visto in (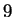 ) possiamo scrivere anche
) possiamo scrivere anche
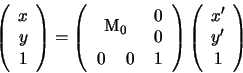 |
(10) |
che applicata in (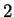 ) ci da:
) ci da:
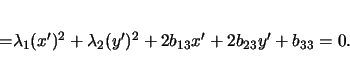 |
(11) |
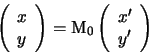
![]() ) nella forma
) nella forma
![]() dove
dove ![]() e
e
![]() non sono simultaneamente nulli. La matrice associata
alla forma è
non sono simultaneamente nulli. La matrice associata
alla forma è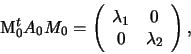
![]() e
e ![]() autovalori di
autovalori di ![]() .
Secondo quanto visto in (
.
Secondo quanto visto in (![]() ) possiamo scrivere anche
) possiamo scrivere anche