Riduzione delle coniche a forma canonica

Consideriamo $\mathbf A^2(\mathbf R)$ , $\mathbf E^2(\mathbf R)$ rispettivamente il piano affine reale, il piano euclideo reale in cui sono fissati dei riferimenti di coordinate

Riprendiamo la definizione di conica:

Definizione 1

Una conica $\mathcal C$ è il luogo dei punti del piano X, Y la cui equazione è della forma:

$\begin{displaymath} a_{11}x^2+a_{22}y^2+2a_{12}xy+2a_{13}x+2a_{23}y+a_{33}=0 \end{displaymath}$

(1)

dove $a_{ij}\in \mathbf R$ e $a_{11}$ , $a_{22}$ , $a_{12}$ non sono contemporaneamente tutti nulli.

Poniamo ora $a_{12}=a_{12}$ , $a_{13}=a_{31}$ , $a_{23}=a_{32}$ e consideriamo le seguenti matrici simmetriche reali

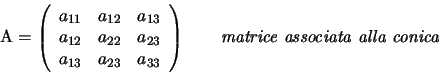
$\begin{displaymath} \mathrm A=\left( \begin{array}{ccc} a_{11} & a_{12} & a_{... ...array} \right) \qquad \textit{matrice associata alla conica} \end{displaymath}$

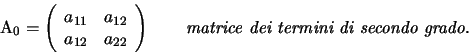
$\begin{displaymath} \hspace{5mm}\mathrm A_0=\left( \begin{array}{cc} a_{11} &... ...\right) \qquad \textit{matrice dei termini di secondo grado}. \end{displaymath}$

Si noti che $\mathrm A_0$ è la matrice della forma quadratica $q(x,y)=a_{11}x^2+2a_{12}xy+a_{22}y^2$ .

Questo ci permette di rappresentare l'equazione () in forma matriciale scrivendo:

$\begin{displaymath} \left( \begin{array}{ccc} x & y & 1 \\ \end{array} \ri... ...eft( \begin{array}{c} x \\ y \\ 1 \end{array} \right)=0. \end{displaymath}$

(2)

Anche il complesso dei termini di secondo grado può essere scritto mediante il prodotto di matrici, ossia:

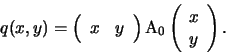$\begin{displaymath} q(x,y)=\left( \begin{array}{cc} x & y \end{array} \righ... ... A_{0} \left( \begin{array}{c} x\\ y \end{array} \right). \end{displaymath}$

(3)

Esempio

Vogliamo ora semplificare il più possibile l'equazione (

) e la tecnica consiste nel cambiare opportunamente il sistema di riferimento (effettuare cioè una trasformazione del piano) euclideo oppure affine.

Diamo ora le seguente definizioni: