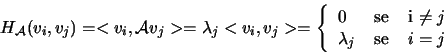
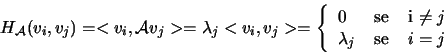
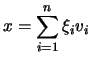Coniche e diagonalizzazione di forme quadratiche

Sia $\mathcal{A}=(a_{ij})$ una matrice simmetrica a coefficienti reali $n\times n$,
consideriamo ora:

$H_\mathcal{A}:\mathbf{R}^n\times \mathbf{R}^n\rightarrow \mathbf{R}$ la forma bilineare ad essa associata,
$Q_\mathcal{A}:\mathbf{R}^n\rightarrow \mathbf{R}$ la forma quadratica ad essa associata.

Per il teorema spettrale, siano $\lambda_1,\ldots,\lambda_n\in\mathbf{R}$ autovalori di $\mathcal{A}$ (tutti reali dato che $\mathcal{A}$ è simmetrica reale) e $v_1,\ldots,v_n\in\mathbf{R^n}$ una base ortonormale di autovettori, tali cioè che $\mathcal{A}v_i=\lambda_iv_i$ con $i=1\ldots n$.
$\forall \,\,x,y\in\mathbf{R}^n$ si può scrivere $H_\mathcal{A}(x,y)=x^t\mathcal{A}y=<x,\mathcal{A}y>$; rispetto alla base di autovettori avremo allora che
\begin{displaymath} H_\mathcal{A}(v_i,v_j)=<v_i,\mathcal{A}v_j>=\lambda_j<v_i,v... ...$\neq j$\\ $\lambda_j$ & se & $i=j$ \end{tabular} \right. \end{displaymath}

da cui si vede che la matrice di $H_\mathcal A$ rispetto alla base $v=(v_1,\ldots,v_n)$, ortonormale, sarà:
\begin{displaymath} {\mathcal D} = \left( \begin{array}{cccc} \lambda_1 & 0 &... ...\vdots \\ 0 & 0 & \cdots & \lambda_n \end{array} \right). \end{displaymath}

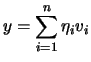Consideriamo ora $x,y\in \mathbf R^n$, rispetto alla base $v$ possiamo scriverli come: $x=\displaystyle\sum_{i=1}^{n} \xi_iv_i$ e $y=\displaystyle\sum_{i=1}^{n} \eta_iv_i$, dove $\xi=(\xi_1,\ldots,\xi_n),\, \eta=(\eta_1,\ldots,\eta_n)\in\mathbf R^n$ sono le coordinate di $x,y$ rispetto alla base $v$. Se sostituiamo otteniamo che
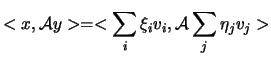 $\displaystyle H_\mathcal A(x,y)$ $\displaystyle =$ $\displaystyle <x, \mathcal Ay>=<\sum_i\xi_iv_i, \mathcal A\sum_j\eta_jv_j>$  
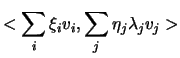  $\displaystyle =$ $\displaystyle <\sum_i\xi_iv_i, \sum_j\eta_j\lambda_jv_j>$  
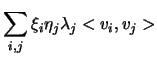  $\displaystyle =$ $\displaystyle \sum_{i,j}\xi_i\eta_j\lambda_j<v_i,v_j>$  
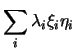$\displaystyle =$ $\displaystyle \sum_i\lambda_i\xi_i\eta_i$  

che è appunto la forma bilineare espressa rispetto ai vettori della base ortonormale. Adesso se prendiamo in considerazione la forma quadratica abbiamo che:

 
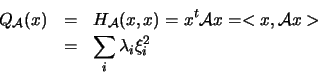
\begin{eqnarray*} Q_\mathcal A(x) &=& H_\mathcal A(x,x)=x^t\mathcal{A}x=<x,\mathcal{A}x>\\ &=& \sum_i\lambda_i \xi_i^2 \end{eqnarray*}

che è la forma quadratica espressa rispetto alla base ortonormale di autovettori. Quindi data una forma quadratica $Q_\mathcal A$, è possibile trovare una base rispetto alla quale $Q_\mathcal A$ ha espressione più semplice: la matrice che la rappresenta è diagonale e $\lambda_1,\ldots,\lambda_n$ sono gli autovalori di $\mathcal A$. Applichiamo quanto detto sin ora allo studio delle coniche e facciamo alcuni esempi che illustrano il procedimento di riduzione a forma canonica di una conica.

Esempio 1 Esempio 2

 

Osservazione 1 Osservazione 2
 

Diamo ora un metodo generale di riduzione a forma canonica e una classificazione generale, sia euclidea che affine

Riduzione a forma canonica