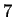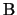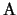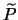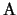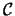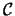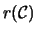Abbiamo ora informazioni sufficienti per dare una prima classificazione delle coniche. Dalla ((x',y',1) tBAB t(x',y',1)) si vede che $\mathrm B$ e $\mathrm A$ hanno lo stesso rango (perchč $\widetilde{P}$ invertibile), quindi il rango di $\mathrm A$ č una proprietą affine della conica $\mathcal C$, che chiameremo il rango di $\mathcal C$, e si denota con $r(\mathcal C)$.

 

Definizione   

La conica 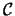$\mathcal C$ č

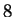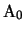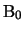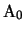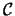Dalla ((x',y',1) ...) si vede anche che $\mathrm A_0$ e $\mathrm B_0$ hanno lo stesso rango e quindi il rango di $\mathrm A_0$ č una proprietą affine di $\mathcal C$. Inoltre poichč
 
\begin{displaymath}det(\mathrm P)=det(\mathrm {P^t})\end{displaymath}

per il teorema di Binet risulta

\begin{displaymath}det (\mathrm B_0)=det(\mathrm {P^tA_0P})=det(\mathrm {P^t})det(\mathrm A_0)det(\mathrm P)\end{displaymath}

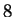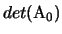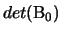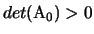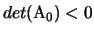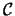e quindi la formula ((x',y',1)...) implica che il segno di $det(\mathrm A_0)$ č lo stesso di quello di $det(\mathrm B_0)$, e quindi anche $det(\mathrm A_0)>0$ e $det(\mathrm A_0)<0$ sono proprietą affini di $\mathcal C$.

Diamo ora il procedimento generale di riduzione a forma canonica affine e euclidea di una conica. Procederemo in diversi passi.
Precedente Passo I